(Miscelânea) Quais das séries abaixo convergem e quais divergem? Justifique suas respostas. (Observação: em alguns casos pode existir mais de uma maneira de determinar a convergência ou divergência da série.)
j)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para dizer se a série converge ou diverge.
Aqui podemos utilizar o Teste da Razão.
Mas que teste é esse?
Então... O Teste da Razão diz que se calcularmos o limite:
Onde é um termo genérico da série e é o que vem depois dele.
Então, temos que:
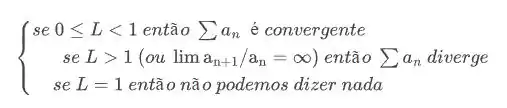
Agora vamos aplicar!! 😉
Passo 2
Assim, fazendo o limite para a série dada, temos:
Simplificando a expressão, temos:
Assim, a série converge pelo Teste da Razão.
Entendeu direitinho? Responde aee ;)

Resposta
A série converge