UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Primeira Lista - 2022.2, Questão 9e
Use o Teste da Raiz para determinar a convergência ou divergência da série dada:
e)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para dizer se a série converge ou diverge pelo Teste da Raiz.
Mas que teste é esse?
Então... O Teste da Raiz diz que se sendo uma série, assumimos que .
Caso esse limite exista, então:
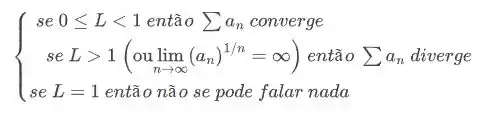
Agora vamos aplicar!! 😉
Passo 2
Assim, fazendo o limite para a série dada, temos:
Tanto o numerador quanto o denominador tendem ao infinito.
Mas o fatorial cresce muito rapidamente quando comparado com o denomidanor. Dessa forma, temos:
Dessa forma, a série converge pelo Teste da Raiz!
Entendeu direitinho? Responde aee ;)
Resposta
A série converge
Exercícios de Livros Relacionados
Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente: ∑ n = 1 ∞ 1 + 1 n n 2
Determine se a série é absolutamente convergente ou condicionalmente convergente. ∑ n = 1 ∞ - 1 n - 1 n n 2 + 4
Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.9. ∑ n = 0 ∞ - 1 n 1,1 n n 4
Prove que, se ∑ a n for absolutamente convergente, então: ∑ n = 1 ∞ a n ≤ ∑ n = 1 ∞ a n
Demonstre o Teste da Raiz. [Sugestão para a parte (i): Tome qualquer número r tal que Lr1 e use o fato de que existe um inteiro N tal que a n nr quando n ≥ N .]