Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 114123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, Tarefas de C3 - Profº Juan Maldonado - 3ª Tarefa, Questão 2

Avalie a integral da superfície ∬ F d S , onde o campo vetorial F é definido por F x , y , z = y i + z - y j + x k , e S é a superfície de tetraedro com vértices (0,0,0), (1,0,0), (0,1,0) e (0,0,1).

Passo 1

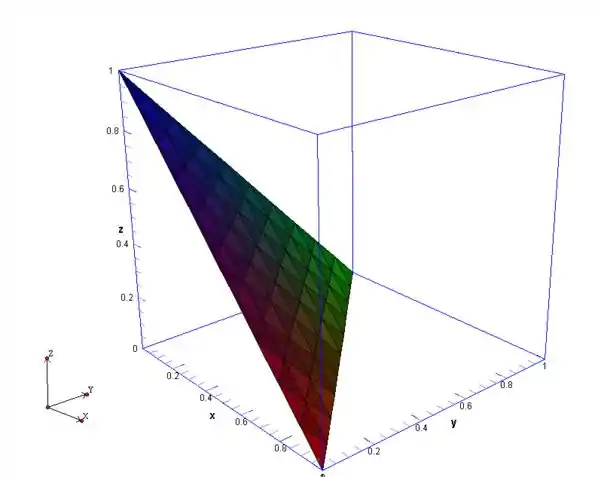
A figura acima representa a nossa superfície, e é sobre ela que iremos realizar a integração.

Passo 2

A superfície é composta por 4 superfícies, S 1 ,   S 2 ,   S 3 , S 4 . Primeiro iremos encontrar o fluxo sobre S 1 . S 1 é parte do plano x = 0 e tem os vértices nos pontos 0,0 , 0 ,   ( 0,1 , 0 ) e ( 0,0 , 1 ) . E uma parametrização para S 1 é

r = 0 i + u j + v k

Onde 0 ≤ u ≤ 1   e 0 ≤ v ≤ 1 - u

r u = j ,   r v = k

r u   x   r v = j   x   k = i

d S =   - r u   x   r v d A =   - i d A

∬ s 1 F ∙ d S = ∫ 0 1 ∫ 0 1 - u ( u i + v - u j + 0 k ) - i d v d u

= ∫ 0 1 ∫ 0 1 - u - u d v d u

= ∫ 0 1 - u 1 - u d u

= ∫ 0 1 u 2 - u d u

= u 3 3 - u 2 2 0 1 = 1 3 - 1 2 = - 1 6

Passo 3

Agora encontrando o fluxo através de S 2 . Utilizaremos a seguinte parametrização para S 2

r = u i + 0   j + v   k

Onde 0 ≤ u ≤ 1 e 0 ≤ v < 1 - u

r u = i

r v = k

r u   x   r v = i   x   k =   - j

Então,

d S = r u   x   r v d A = - j d A

∬ S 2 F ∙ d S = ∫ 0 1 ∫ 0 1 - u 0   i + v - 0 j + u k ∙ - j d v d u

= ∫ 0 1 ∫ 0 1 - u - v d v d u = ∫ 0 1 - 1 - u 2 2 d u  

= ∫ 0 1 - u 2 2 d u = u 3 6 0 1 = - 1 6

Passo 4

O fluxo agora através de S 3 , que é parte do plano z = 0 com os vértices ( 1,0 , 0 ) , ( 0,1 , 0 ) e ( 0,0 , 0 ) .

A parametrização para S 3 é

r = u i + v j + 0 k

Onde 0 ≤ u ≤ 1 e 0 ≤ v ≤ 1 - u .

r u = i

r v = j

r u   x   r v = i   x   j = k

Então temos

d S =   - r u   x   r v d A =   - k d A

∬ S 3 F ∙ d S = ∫ 0 1 ∫ 0 1 - u v   i + 0 - v j + u   k - k d v d u

= ∫ 0 1 ∫ 0 1 - u - u d v d u = ∫ 0 1 - u 1 - u d u

= ∫ 0 1 u 2 - u   d u = u 3 3 - u 2 2 0 1 = 1 3 - 1 2 = - 1 6

Passo 5

Agora iremos finalmente calcular a última integral, da superfície S 4 , e para isso iremos utilizar a formula

∬ S F ∙ d S = ∬ D - P ∂ g ∂ x - Q ∂ g ∂ y + R d A

Onde F = P i + Q j + R k e D é a projeção de S no plano xy.

∬ S 4 F ∙ d S = ∫ 0 1 ∫ 0 1 - x - y - 1 - z - y - 1 + x d y d x

= ∫ 0 1 ∫ 0 1 - x y + z - y + x d y d x

= ∫ 0 1 ∫ 0 1 - x z + x d y d x

Substituindo z = 1 - x - y

= ∫ 0 1 ∫ 0 1 - x 1 - y   d y d x

= ∫ 0 1 y - y 2 2 0 1 - x d x

= ∫ 0 1 1 - x - 1 - x 2 2 d x

= ∫ 0 1 x - x 2 2 d x

= x 2 2 - x 3 6 0 1

= 1 2 - 1 6 = 1 3

Agora calculando o fluxo total

- 1 6 - 1 6 - 1 6 + 1 3 = - 1 6

Resposta

- 1 6

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1