Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 103123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcular a área da parte da superfície z 2 = y 2 - x 2 situada entres os planos

y = 1 2 x + 3   e   y = 0 .

Passo 1

A superfície z 2 = y 2 - x 2 pode ser escrita como y 2 = x 2 + z 2 ,   a qual é um cone com o eixo y. Pra você ver isso é bem tranquilo! Separa de lados opostos da igualdade quem tem sinais opostos. Ficamos então com

z 2 = y 2 - x 2 → y 2 = x 2 + z 2

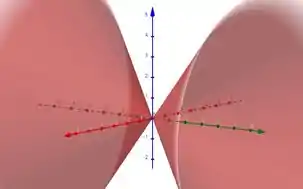
Ficamos então com esse cone que cresce na direção de y .

Observa que somente queremos a área do cone na parte positiva de y , limitada pelo plano y = 1 2 x + 3 , como nos foi passado no enunciado.

Passo 2

Bora calcular a interseção do cone y 2 = x 2 + z 2 com o plano y = 1 2 x + 3

1 4 x 2 + 3 x + 9 = 1 2 x + 3 2 = y 2

y 2 = x 2 + z 2

1 4 x 2 + 3 x + 9 = x 2 + z 2

Completando o quadrado

x - 2 2 16 + z 2 12 = 1

Achamos a equação de uma elipse.

Passo 3

Vamos então agora parametrizar nossa superfície. Uma parametrização legal seria uma parametrização explícita mesmo.

x = x

z = z

y = x 2 + z 2

Logo

ϕ x , z = x ,   x 2 + z 2 ,   z

Lembrando que o domínio vai ser x - 2 2 16 + z 2 12 ≤ 1  

Passo 4

Vamo calcular agora o módulo do vetor normal

∂ ϕ ∂ x = 1 ,   - x x 2 + z 2 ,   0

∂ ϕ ∂ z = 0 ,   - y x 2 + z 2 ,   1

N = i j k 1 x x 2 + z 2 0 0 z x 2 + z 2 1 = x x 2 + z 2 i + z x 2 + z 2 k - j

N = x 2 + z 2 x 2 + z 2 + 1 = 1 + 1 = 2

Passo 5

Assim nossa área procurada fica sendo

A = ∬ D N d x d z = ∬ D 2 d x d z

Lembrando que D

x - 2 2 16 + z 2 12 = 1

E sua área é dada por

A D = 16 × 12 × π

Logo

= 2 . A D = 2 × 16 × 12 × π = 8 6 π

Resposta

8 6 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1