4) Calcule a área das Superfícies:

b) Parte da esfera , interior ao cone

Agora temos que fazer a limitação da nossa região de integração, mas como vamos fazer isso? Vamos ver em que lugar a esfera corta o cone e tentar tirar por aí os limites, repara que temos algo assim

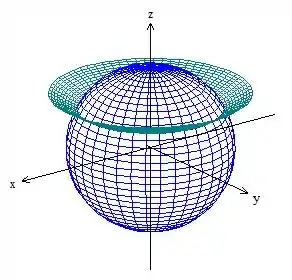
Isso nos diz que vai dar uma volta inteira, o que está sendo limitado é , então

Vamos ver quando eles se encontram

Substituindo isso na equação da esfera vamos ter

Estamos pegando o valor positivo de porque por ser uma raiz positiva.

Usando as coordenadas esféricas vamos ter

O ângulo que tem cosseno igual a é que vai ser, em radianos,

Então vamos ter

Aplicando a fórmula da integral de superfície:

Já sabemos quanto dá esse vetor normal da esfera, mas por prática nós vamos calcular tudo, começando pelas derivadas parciais:

Calculando o produto vetorial:

Fica uma dica aqui: você pode fatorar do determinante do produto vetorial um termo de uma linha ou coluna dele. No caso nunca vamos fatorar as colunas porque o primeiro elemento é sempre um vetor (), mas de resto esse truque é bastante útil. Na última linha podemos fatorar o :

Pra quem acha que vai ajudar também pode fatorar da segunda linha o , lembrando que vai sobrar na última coluna. Eu não acho tão útil assim porque pode confundir mais depois, mas fica à critério de cada um. Seguindo:

Fazendo a distributiva do que nós pusemos em evidência lá em cima:

Buscando o módulo dessa monstruosidade:

It’s Algebra Time, baby! Pondo em evidência:

Pondo em evidência:

Como o ângulo , por definição, pertence ao intervalo ele nunca é negativo, portanto:

Finalmente, podemos plugar os valores dos limites de integração na fórmula.