6) Calcule o fluxo do campo , através da superfície do sólido limitado pelo cilindro e pelos planos e , com a normal apontando para fora do sólido.
Passo 1
Se o problema nos pediu fluxo de sobre uma superfície , com toda certeza o que ele está buscando é que façamos uma integral de superfície:
Para resolver essa integral, poderíamos seguir basicamente 2 caminhos:
1º - Fazer de uma forma direta (parametrizando e tudo mais)
2º - Aplicar o Teorema de Gauss.
Veja você que embora o campo é um pouco simpático com a gente, a superfície é uma superfície composta por outras três superfícies diferentes entre si, dois plano e um cilindro...
O fato de ter uma superfície composta já é uma indicação de que vamos ter que pegar o segundo caminho, ou seja, resolver pelo Teorema de Gauss. Mas, se você quer mais certeza ainda, calcule o divergente...
Como
Calculando as derivadas parciais:
Logo...
Pow, com um divergente simples desses... Sim, o problema está pedindo que façamos por Gauss!
Passo 2
O teorema basicamente é a igualdade maravilhosa:
Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma superfície fechada delimitando o sólido :
Como vimos, o sólido é:
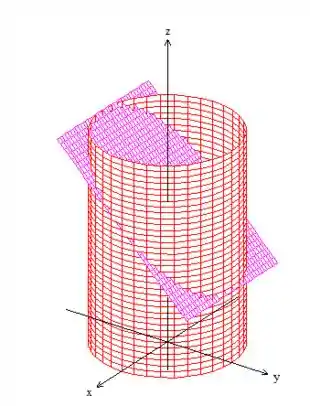
Yes! A superfície é fechada.
2º - Sem singularidades na função Vetorial:
Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por ou algo do tipo.
3º - Superfície orientada positivamente:
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado.
Passo 3
Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...
Então se queremos a integral de superfície, calculemos a integral tripla que cara, vai dar muito menos trabalho, acredita em mim!
Passo 4
Como estamos falando de um pedaço de um cilindro, podemos utilizar as mudanças para coordenadas cilíndricas:
Onde o Jacobiano dessa mudança é:
E uma equação que nos ajuda muito é a equação do cilindro:
Passo 5
Não devemos sair de uma mudança de coordenadas sem antes dizer onde os parâmetros variam:
Para encontrar a variação de e , devemos olhar pra projeção do sólido no plano ...
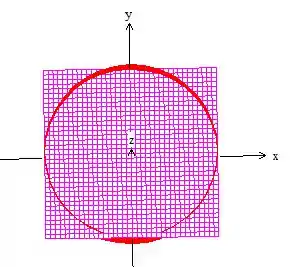
Veja que o raio varia dentro da superfície desde a origem até o raio máximo do cilindro que é ...
E o ângulo , bem, esse cara tá dando uma volta completa...
Já variação do , bem ele é o cara que varia de cima pra baixo no sólido:
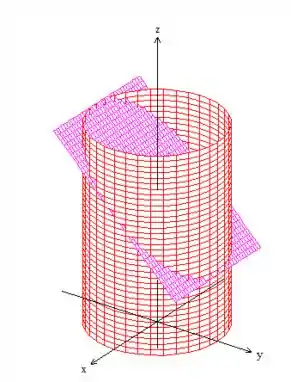
Ou seja...
Isolando...
Como agora estamos em outras coordenadas...
Passo 6
Retornando à integral que queremos resolver...
Onde vamos substituir tudo, não se esquecendo de colocar o Jacobiano...
Calculando a integral de dentro...
Simplificando isso mais um pouco...
E integrando em ...
Lembre-se que...
Então...
Ent��o pelo teorema de Gauss, o fluxo é...