Calcule a integral de superfície
Onde é a parte do parabolóide hiperbólico dentro do parabolóide .
Passo 1
A questão já quer nos assustar falando de paraboloide hiberbólico e sei lá mais o que, mas fica tranquilo que não tem mistério não, é só seguir o passo-a-passo!
Primeiro temos uma integral de superfície escalar, então só temos a opção de usar a fórmula:
Agora só falta entender melhor essa superfície ai, pra tentarmos encontrar uma parametrização boa e calcularmos o normal.
Passo 2
O parabolóide hiperbólico é aquela famosa “sela de cavalo”, mas essa aqui está centrada em , então fica ainda mais estranha, vamos ver:
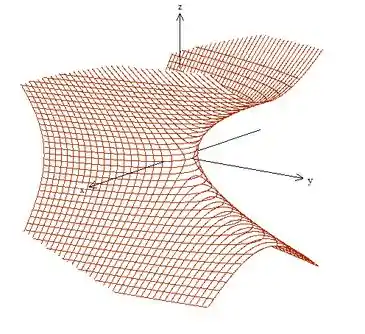
Não ajuda muito fazermos nenhuma parametrização clássica, então vamos usar a explícita mesmo, mas em , porque ele é o mais fácil de isolar:
E a parametrização fica:
Com o domínio sendo a projeção no plano da interseção com o parabolóide:
O que parece relativamente tranquilo.
Agora vamos ver o vetor normal!
Passo 3
Como temos a parametrização explícita, não precisamos fazer conta nenhuma, é só lembrar que, se :
Então tirando o módulo, vamos ter:
Agora é só jogar na fórmula!
Passo 4
Já temos tudo o que precisamos pra fazer:
Calma! Eu sei que parece uma conta bizarra, mas vai tudo simplificar, quer ver?
Opa! Agora parece que vai!
Agora chegamos numa integral dupla molezinha, é só partir pro abraço!
Passo 5
Vamos lembrar que nosso domínio era:
Então coordenadas polares parece uma ótima ideia, né? Não tem muita diferença, mas como aqui temos , vamos fazer:
E o domínio vai ser, simplesmente:
Então, vamos ter:
Um valor meio estranho, mas nada dos mais bizarros também.