Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 116123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

9) Calcule

∬ S   f x ,   y   d S

Onde

e) f x ,   y ,   z = x 2 + y 2 + z 2 e S é a porção da esfera x 2 + y 2 + z 2 = 36 , limitada pelos planos z = 0 e z = 3 .

Passo 1

Estamos lidando nesse caso com uma integral de linha no caso escalar onde para resolver, seguiremos o passo a passo para a sua solução direta:

1º - Parametrizar a superfície S .

2º - Substituir os termos da parametrização na função f x ,   y ,   z .

3º - Encontrar o termo d S .

Partiu chegar ao nosso objetivo?

Passo 2

Bem, primeiro, como vimos, devemos parametrizar a superfície S . Porém, Quem é essa superfície? Como o próprio exercício nos indicou a parte da esfera de raio 6 , mas delimitada pelos planos z = 0 e z = 3 ...

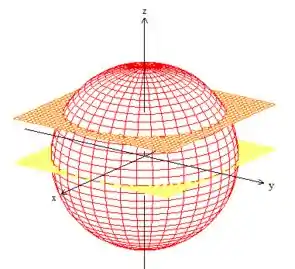
Hmmm! Superfície esférica não nos parece uma má ideia parametriza-la com as primas das coordenadas polares com a diferença que o raio é 6 :

x = 6 sin ⁡ ϕ cos ⁡ θ

y = 6 sin ⁡ ϕ sin ⁡ θ

z = 6 cos ⁡ ϕ

Ou, com uma anotação um pouco mais elegante do ponto de vista da matemática...

r → ϕ ,   θ = 6 sin ⁡ ϕ cos ⁡ θ , 6 sin ⁡ ϕ sin ⁡ θ ,   6 cos ⁡ ϕ

Passo 3

Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.

Bem, como a parametrização é prima das coordenadas esféricas, o ângulo θ gira no plano x y ao redor do eixo z :

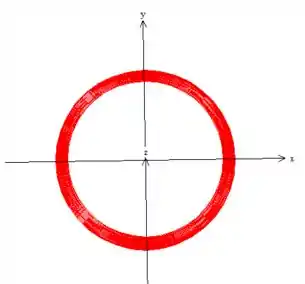
Como pode ver na projeção da superfície no plano x y , precisamos de um θ dando uma volta completa:

0 ≤ θ ≤ 2 π

Passo 4

O ângulo ϕ , que sai do eixo z descendo, entra na superfície onde o plano z = 3 cortou e sai no z = 0

P l a n o   z = 3   ≤ ϕ ≤ P l a n o   z = 0

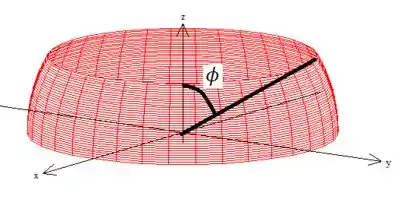
Substituindo o z pelo termo da parametrização...

      z = 3   →       6 cos ⁡ ϕ = 3         →         cos ⁡ ϕ = 1 2

Nesse caso o ϕ só pode ser 60 ° = π 3 ...

π 3 ≤ ϕ ≤ P l a n o   z = 0

Fazendo o mesmo para...

z = 0   →       6 cos ⁡ ϕ = 0   →     cos ⁡ π = 0

Nesse caso o ϕ só pode ser 90 ° = π 2 ...

π 3 ≤ ϕ ≤ π 2

Passo 5

Então, agora precisamos substituir os termos da função que estamos integrando...

f x ,   y ,   z = x 2 + y 2 + z 2

Poderíamos simplesmente trocar os termos x , y e z ali dentro pelos termos da parametrização. Mas isso daria muita conta! Podemos poupar tempo se percebemos que a esfera S tem equação x 2 + y 2 + z 2 = 36 ...

f x ,   y ,   z = 36   →       f x ,   y ,   z = 6

Passo 6

Beleza, então com essas etapas concluídas, podemos sair em busca do termo d S ...

d S = N →   d ϕ d θ

Onde esse vetor normal é dado por...

N → = ∂ r → ϕ ,   θ ∂ ϕ × ∂ r → ϕ ,   θ ∂ θ

Não precisa se preocupar com a ordem dessas derivadas parciais, pois o módulo no d S corrige qualquer sinal de menos ( ). Por falar nisso, calculando essas derivadas parciais...

r → ϕ ,   θ = 6 sin ⁡ ϕ cos ⁡ θ , 6 sin ⁡ ϕ sin ⁡ θ ,   6 cos ⁡ ϕ

  ∂ r → ϕ ,   θ ∂ ϕ = 6 cos ⁡ ϕ cos ⁡ θ ,   6 cos ⁡ ϕ sin ⁡ θ ,   - 6 sin ⁡ ϕ

∂ r → ϕ ,   θ ∂ θ = - 6 sin ⁡ ϕ sin ⁡ θ , 6 sin ⁡ ϕ cos ⁡ θ ,   0

Substituindo tudo dentro do produto vetorial (um determinante, lembrando que a primeira linha são os vetores i → , j → e k → )...

N → = ∂ r → u ,   v �� u × ∂ r → u ,   v ∂ v

N → = i → j → k → 6 cos ⁡ ϕ cos ⁡ θ 6 cos ⁡ ϕ sin ⁡ θ - 6 sin ⁡ ϕ - 6 sin ⁡ ϕ sin ⁡ θ 6 sin ⁡ ϕ cos ⁡ θ 0     ��           →

N → = 36 sin 2 ⁡ ϕ sin ⁡ θ j → + 36 cos ⁡ ϕ sin ⁡ ϕ cos 2 ⁡ θ k → - - 36 sin 2 ⁡ ϕ cos ⁡ θ i → - 36 cos ⁡ ϕ sin ⁡ ϕ sin 2 ⁡ θ k →   →

N → = 36 sin 2 ⁡ ϕ sin ⁡ θ j → + 36 cos ⁡ ϕ sin ⁡ ϕ cos 2 ⁡ θ k → - - 36 sin 2 ⁡ ϕ cos ⁡ θ i → - 36 cos ⁡ ϕ sin ⁡ ϕ sin 2 ⁡ θ k →   →

N → = 36 sin 2 ⁡ ϕ cos ⁡ θ i → + 36 sin 2 ⁡ ϕ sin ⁡ θ j → + 36 cos ⁡ ϕ sin ⁡ ϕ cos 2 ⁡ θ k → + 36 cos ⁡ ϕ sin ⁡ ϕ sin 2 ⁡ θ k →   →

N → = 36 sin 2 ⁡ ϕ cos ⁡ θ i → + 36 sin 2 ⁡ ϕ sin ⁡ θ j → + 36 cos ⁡ ϕ sin ⁡ ϕ ( cos 2 ⁡ θ + sin 2 ⁡ θ )   k →   →

N → = 36 sin 2 ⁡ ϕ cos ⁡ θ i → + 36 sin 2 ⁡ ϕ sin ⁡ θ j → + 36 cos ⁡ ϕ sin ⁡ ϕ )   k →  

Logo...

N → = 36 sin 2 ⁡ ϕ cos ⁡ θ ,   36 sin 2 ⁡ ϕ sin ⁡ θ ,   36 cos ⁡ ϕ sin ⁡ ϕ

Como queremos o módolo...

N → = 36 sin 2 ⁡ ϕ cos ⁡ θ 2 + 36 sin 2 ⁡ ϕ sin ⁡ θ 2 + 36 cos ⁡ ϕ sin ⁡ ϕ 2   →

N → = 36 2 sin 4 ⁡ ϕ cos 2 ⁡ θ + 36 2 sin 4 �� ϕ sin 2 ⁡ θ + 36 2 cos 2 ⁡ ϕ sin 2 ⁡ ϕ   →

N → = 36 2 sin 4 ⁡ ϕ cos 2 ⁡ θ + sin 2 ⁡ θ + 36 2 cos 2 ⁡ ϕ sin 2 ⁡ ϕ   →

N → = 36 2 sin 4 ⁡ ϕ + 36 2 cos 2 ⁡ ϕ sin 2 ⁡ ϕ   →

N → = 36 2 sin 2 ⁡ ϕ cos 2 ⁡ ϕ + sin 2 ⁡ ϕ   →

N → = 36 2 sin 2 ⁡ ϕ   →

Como o ϕ é menor que 90 ° , o seu seno é positivo, logo...

N → = 36 sin ⁡ ϕ

d S = 36 sin ⁡ ϕ   d ϕ d θ

Passo 7

Voltando para integral de linha que estamos resolvendo...

∬ S   f x ,   y ,   z d S

E substituindo esses termos que determinamos (lembrando que S , trocamos por D que é a região de variação de ϕ e θ ).

∬ S   f x ,   y ,   z d S = ∬ D   6 ⋅ 36 sin ⁡ ϕ   d ϕ d θ =

∫ 0 2 π ∫ π 3 π 2 6 ⋅ 36 sin ⁡ ϕ   d ϕ d θ =

216 ∫ 0 2 π ∫ π 3 π 2 sin ⁡ ϕ   d ϕ d θ =

216 ∫ 0 2 π - cos ⁡ π 2 - - cos ⁡ π 3 d θ =

216 ∫ 0 2 π 1 2 d θ = 216 2 ∫ 0 2 π d θ =

216 2 ⋅ 2 π =

216 π

Resposta

216 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1