Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 115123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

9) Calcule

∬ S   f x ,   y , z   d S

Onde

e) f x ,   y ,   z = x 2 y 2 z 2 e S é a parte da superfície cônica z = x 2 + y 2 , limitada por z = 4 - x 2 + y 2 , com z ≥ 0 .

Passo 1

Estamos lidando nesse caso com uma integral de linha no caso escalar onde para resolver, seguiremos o passo a passo para a sua solução direta:

1º - Parametrizar a superfície S .

2º - Substituir os termos da parametrização na função f x ,   y ,   z .

3º - Encontrar o termo d S .

Partiu chegar ao nosso objetivo?

Passo 2

Bem, primeiro, como vimos, devemos parametrizar a superfície S . Porém, Quem é essa superfície?

Bem, estamos trabalhando com um cone limitado por outro, com a boca pra baixo:

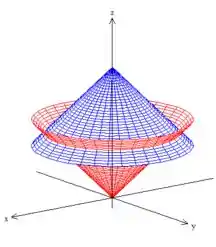
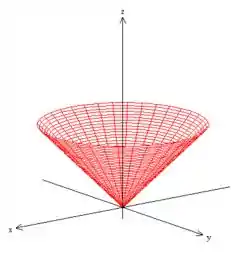
Como estamos trabalhando com uma superfície em cima de um cone de equação explícita

z = x 2 + y 2

Podemos pensar em uma parametrização explícita, tal que os dois parâmetros sejam o próprio x e y ...

r → x ,   y = x ,   y ,   x 2 + y 2

Passo 3

Como toda e qualquer parametrização, necessitamos de determinar onde é que os parâmetros x e y estão variando.

Bem, x e y varia na limitação imposta pelo problema, na intercessão dos dois cones. Fazer uma intersecção em matemática é resolver o sistema:

z = x 2 + y 2 z = 4 - x 2 + y 2   →

4 - x 2 + y 2 = x 2 + y 2   →

2 x 2 + y 2 = 4   →

x 2 + y 2 = 4 2 = 2

Repare que falar que a superfície está delimitada por esse cone de cabeça pra baixo é um jeito mais complicado de dizer que ele está delimitado pelo plano z = 2 .

Se olharmos para a projeção desse sólido no plano x y , veremos uma circunferência, que é exatamente a circunferência de raio 2 ,   x 2 + y 2 = 2 .

Por hora, podemos simplesmente indicar que x e y estão dentro dessa região D aí, apenas para não perder o foco na integral de superfície ;)

x ,   y ∈ D

Passo 4

Então, agora precisamos substituir os termos da função que estamos integrando...

f x ,   y ,   z = x 2 y 2 z 2

Como

r → x ,   y = x ,   y ,   x 2 + y 2

f r → x ,   y = x 2 y 2 x 2 + y 2

Passo 5

Beleza, então com essa primeira etapa já resolvida podemos sair em busca do termo d S ...

d S = N →   d x d y

Onde esse vetor normal é dado por...

N → = ∂ r → x , y ∂ x × ∂ r → x , y ∂ y

Mas como parametrizamos como z em função explícita de x e y , ou melhor, como um gráfico de função, podemos usar o bizu de vetor normal nessas condições e ganhar tempo...

N → = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1

como

z = x 2 + y 2

∂ z ∂ x = 1 2 x 2 + y 2 ⋅ ∂ x 2 + y 2 ∂ x = x x 2 + y 2

∂ z ∂ y = 1 2 x 2 + y 2 ⋅ ∂ x 2 + y 2 ∂ y = y x 2 + y 2

Então...

N → = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1 = - x x 2 + y 2 ,   - y x 2 + y 2 ,   1

Calculando o módulo...

N → = - x x 2 + y 2 2 + - y x 2 + y 2 2 + 1 2   →

N → = x 2 x 2 + y 2 + y 2 x 2 + y 2 + 1 →

N → = x 2 + y 2 x 2 + y 2 + 1   →

N → = 1 + 1 = 2

d S = 2   d x   d y

Passo 6

Passo 7

Voltando para integral de linha que estamos resolvendo...

∬ S   f x ,   y ,   z   d S

E substituindo esses termos que determinamos (lembrando que S , trocamos por D que é a região de variação de x e y ).

A s = ∬ S   f x ,   y ,   z   d S = ∬ D     x 2 y 2 x 2 + y 2 ⋅ 2   d x   d y

Como estamos em uma região circular

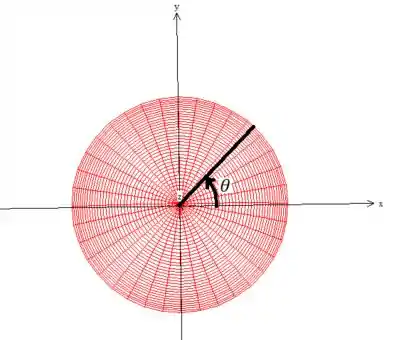
E trabalhando com somas de coisas ao quadrado, podemos pensar em uma mudança para coordenadas polares...

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

x 2 + y 2 = r 2

Onde r varia de 0 até o raio máximo que é o raio de D ...

0 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

Substituindo tudo...

∬ D     x 2 y 2 x 2 + y 2 ⋅ 2   d x   d y = ∫ 0 2 π ∫ 0 2 r cos ⁡ θ 2 r sin ⁡ θ 2 r 2 ⋅ 2   J   d r d θ

2 ∫ 0 2 π ∫ 0 2 r 7 cos 2 ⁡ θ sin 2 ⁡ θ     d r d θ

Calculando a integral em r considerando θ constante...

2 ∫ 0 2 π cos 2 ⁡ θ sin 2 ⁡ θ ∫ 0 2 r 7 d r d θ =

2 ∫ 0 2 π cos 2 ⁡ θ sin 2 ⁡ θ r 8 8 0 2 d θ =

2 ∫ 0 2 π cos 2 ⁡ θ sin 2 ⁡ θ 2 8 2 3 d θ =

32 2 ∫ 0 2 π cos 2 ⁡ θ sin 2 ⁡ θ d θ =

Substituindo sin 2 ⁡ θ = 1 - cos 2 ⁡ θ ...

32 2 ∫ 0 2 π cos 2 ⁡ θ 1 - cos 2 ⁡ θ d θ =

32 2 ∫ 0 2 π cos 2 ⁡ θ - cos 4 ⁡ θ d θ =

Considerando que cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 ...

32 2 ∫ 0 2 π 1 + cos ⁡ 2 θ 2 - 1 + cos ⁡ 2 θ 2 2 d θ =

32 2 ∫ 0 2 π 1 + cos ⁡ 2 θ 2 - 1 4 1 + 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ d θ =

E agora considerando que cos 2 ⁡ 2 θ = 1 + cos ⁡ 4 θ 2 ...

32 2 ∫ 0 2 π 1 2 + cos ⁡ 2 θ 2 - 1 4 1 + 2 cos ⁡ 2 θ + 1 + cos ⁡ 4 θ 2 d θ =

32 2 ∫ 0 2 π 1 2 + cos ⁡ 2 θ 2 - 1 4 - 1 2 cos ⁡ 2 θ - 1 + cos ⁡ 4 θ 8 d θ =

32 2 ∫ 0 2 π 1 4 - 1 8 - cos ⁡ 4 θ 8 d θ =

32 2 ∫ 0 2 π 1 8 - cos ⁡ 4 θ 8 d θ =

32 2 1 8 θ - sin ⁡ 4 θ 32 0 2 π =

32 2 1 8 ⋅ 2 π =

8 2 π

Resposta

8 2 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1