Considere a superfície .
- Esboce a superfície .
- Parametrize a superfície .
- Determine o vetor normal unitário no ponto que aponta para cima.
- Calcule a área de .
Passo 1
- Muito bem, antes de baixar o nosso Pablo Picasso interior e desenhar essa superfície, vamos começar entendendo quem os elementos dessa superfície.
- Bem, como já temos aqui uma função bem comportada em termos de outros dois termos, , podemos então pensar em uma parametrização explícita, se lembra?
- Vamos começar encontrando os vetores normais a superfície , .
- Então, calcular a área de uma superfície para a gente é calcular uma integral de superfície...
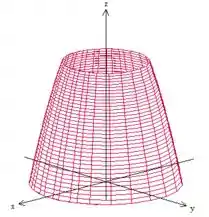
O primeiro deles é . Essa equação nos representa um paraboloide, como e estão negativos, nos sugere que é um paraboloide com a boca para baixo, dessa forma aqui:
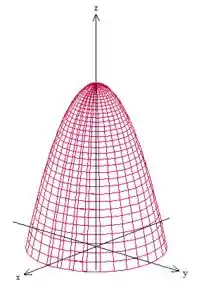
Esse ponto onde o paraboloide aí toca o eixo é quando são , então , ou seja , pegou a ideia?
Bem, mas não queremos o paraboloide todo. Queremos apenas o que obedece a essa outra condição aqui: .
indica que a gente quer a parte do paraboloide acima do plano , mas e esse ?
Se você se lembrar, é um plano paralelo ao que passa por . Esse Plano está cortando o paraboloide em duas partes
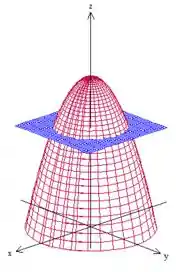
A superfície que queremos é justamente essa parte abaixo do plano. :D
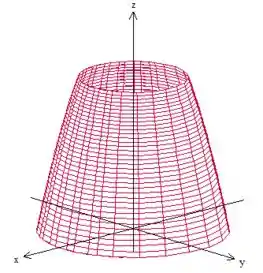
Passo 2
Nessa parametrização, a gente chama
E então...
A parametrização então ficará
Beleza?:)
Mas tem um detalhe! Toda parametrização precisamos determinar qual é a variação de dos novos parâmetros, o que no caso é e . Bora lá?
Passo 3
Bem, como e variam em cima de e , é legal a gente olhar para a projeção da superfície no plano . Assim seremos capazes de descrever a região onde e varia, percebeu?
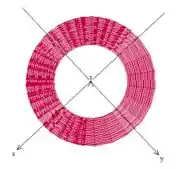
Fazendo a projeção no plano , teremos:
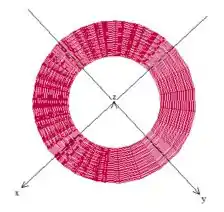
Repare que e variam nesse anel circular, logo e também variará!
Passo 4
Pra encontrar os limites desse anel, lembre-se que esse raio menor foi determinado pelo corte do plano , logo como , teremos
Esse representa o raio inferior, para encontrar o superior do anel, utilizamos a equação do outro plano que delimita a superfície, , ou seja:
Logo, e variam nessa região que chamaremos de , entre essas duas circunferências de raio e
Passo 5
Como parametrizamos na forma explicita podemos aplicar o bizu de vetor normal dessa forma aqui
Calculando as derivadas parciais...
Obteremos
Passo 6
Bem, aplicando o vetor normal no ponto pedido , como e , basta substituir e ...
Agora, calculando o vetor unitário pela fórmula...
Onde o é a norma desse vetor e vale a raiz das soma dos termos ao quadrado do vetor
Ou seja
Multiplicando cada uma dessas entradas por essa constante
Passo 7
Lembrando que , podemos trocar a integral de superfície, peal integral dupla:
O vetor já foi encontrado e como já vimos, podemos encontrar assim:
Colocando em evidência...
Passo 2
Bem, substituindo agora na integral dupla
e lembrando que a região de integração é aquele anel, podemos fazer uma mudança para coordenadas polares...
Uma equação que nos ajuda muito aqui é a do círculo:
Onde o raio, a gente viu que varia do menor até o maior raio que a gente já determinou no passo 4, se lembra?:)
E o ângulo theta, bem... ele dar uma volta completa, logo
Passo 3
Substituindo na integral que devemos calcular
Resolvendo primeiro a integral de dentro fazendo uma substituição simples
Não se esqueça de mudar os limites também, hem!
Teremos
Integrando em passando essa constante pro lado de fora da integral
Substituindo os limites de integração
Colocando o termo em evidência e passando para fora da integral
Passando para fora o e integrando em
Resposta
a)
b)
c)
d)