Determine a área da lâmina do cilindro circular em contida entre o plano e o cilindro parabólico , no primeiro octante.
Passo 1
Bom, vamos começar desenhando isso aí para entender melhor. Temos um cilindro circular de raio e um cilindro parabólico.
O primeiro é tranquilo de desenhar, né. O segundo, nós podemos pensar que é uma parábola no plano que se “repete” ao longo do eixo , dessa forma:
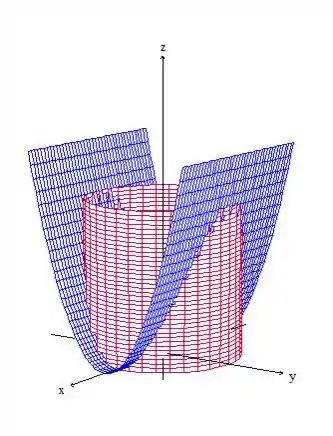
Foi? O problema pede a área do cilindro vermelho que está contida entre o cilindro azul e o plano , considerando apenas o primeiro octante. OI??? Calma, vamos fazer um outro desenho para entender melhor:
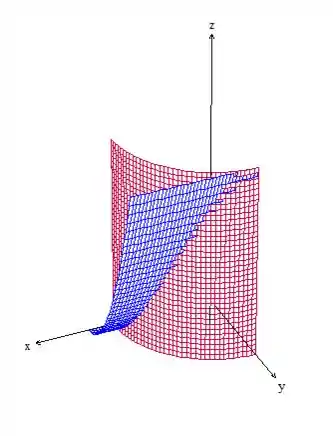
Aqui temos só o 1º octante, portanto já nos livramos dessa parte. Como o problema quer a parte da superfície vermelha entre a azul e o plano , queremos a parte do cilindro circular abaixo do cilindro parabólico.
Portanto, a superfície da questão é esse retalho do cilindro vermelho que está mais próximo da gente (abaixo da superfície azul e acima do plano ).
Passo 2
Show? Agora, para calcular a área dessa superfície, temos que começar parametrizando ela.
Como se trata de um cilindro, vamos usar coordenadas cilíndricas:
Já que o raio do cilindro é , temos:
Beleza? Agora vamos pensar nos intervalos desses parâmetros, e . Como o enunciado diz, a superfície está contida no 1º octante, portanto .
A variável , nós podemos ver que está entre o plano , onde e a o cilindro parabólico, onde , que, em coordenadas cilíndricas é:
Portanto, temos .
Passo 3
Agora, precisamos calcular e
Passo 4
Calcular o módulo da normal
Passo 5
Agora temos que montar a integral, temos:
Substituindo:
Agora vamos substituir os intervalos que encontramos na parametrização:
Passo 6
Beleza, agora é só resolver isso aí:
Aqui temos que usar a seguinte fórmula trigonométrica: