Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 142123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 4ª Lista, Questão 11

Nos exercícios 05 → 15 , calcule a área da superfície S .

11. S é a superfície do cilindro 2 z = x 2 , cortada pelos planos 2 y = x , y = 2 x e x = 2 2 .

Passo 1

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema queremos calcular a área da superfície 2 z = x 2 que está entre os planos 2 y = x , y = 2 x e x = 2 2 .

Lembra como podemos fazer isso? 😬

Para calcular a área de uma superfície parametrizada podemos aplicar uma formulinha dada por

∫ ∫ S 1 d S

Onde d S pode ser obtido como N → d A e N → é o vetor normal à superfície...

Para obter o vetor normal N → podemos derivar a função vetorial σ parcialmente em relação às suas parametrizações e calcular o produto vetorial dos vetores obtidos.

Sacou? Bora começar! 😉

Passo 2

Nesse caso, como a região que limita nossa superfície é cartesiana, podemos parametrizar a nossa curva a partir das coordenadas cartesianas mesmo... x continua sendo x , y sendo y e z podemos isolar em um lado da igualdade e defini-lo em função de x .

2 z = x 2 → z = x 2 2

Portanto, temos que

σ ( x , y ) = x , y , x 2 2

Começamos calculando o vetor normal a superfície primeiro derivando σ em relação a x ...

σ x = ∂ x ∂ x , ∂ y ∂ x , ∂ x 2 2 ∂ x

σ x = 1 , 0 , x

Agora com relação a y ...

σ y = ∂ x ∂ y , ∂ y ∂ y , ∂ x 2 2 ∂ y

σ y = 0 , 1 , 0

Calculando o produto vetorial entre σ x e σ y ...

N → = σ x × σ y = i j k 1 0 x 0 1 0

N → = x , 0 , 1

Calculando o modulo desse vetor, temos

N → = x 2 + 0 2 + 1 2

N → = x 2 + 1

Tranquilo até aqui? 😊

Passo 3

Só nos resta saber como vamos definir d A ...

Pra isso podemos olhar para a projeção da nossa região no plano x y , ou seja, podemos olhar de cima e definir como x e y varia...

Esboçando 2 y = x , y = 2 x e x = 2 2 no plano cartesiano, temos

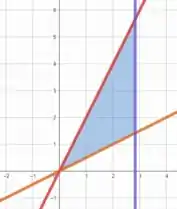
Com isso podemos definir que y varia no intervalo x 2 ≤ y ≤ 2 x .

E vemos também que x varia no intervalo 0 ≤ x ≤ 2 2

Dessa forma d A = d y d x .

Substituindo essas informações na integral e aplicando os limites de integração, temos

∫ ∫ S 1 d S → ∫ 0 2 2 ∫ x 2 2 x x 2 + 1 d y d x

Integrando com relação a y ...

∫ x 2 + 1 d y = x 2 + 1 y

Aplicando os limites de integração

∫ x 2 2 x x 2 + 1 d y = x 2 + 1 2 x - x 2 + 1 x 2

∫ x 2 2 x x 2 + 1 d y = 2 x x 2 + 1 - x x 2 + 1 2

Integrando o resultado em função de x pelo método de substituição.

∫ 2 x x 2 + 1 - x x 2 + 1 2 d x = 2 x 2 + 1 3 2 3 - x 2 + 1 3 2 6

Aplicando os limites de integração

∫ 0 2 2 2 x x 2 + 1 - x x 2 + 1 2 d x = 2 2 2 2 + 1 3 2 3 - 2 2 2 + 1 3 2 6 - 2 0 2 + 1 3 2 3 - 0 2 + 1 3 2 6

∫ 0 2 2 2 x x 2 + 1 - x x 2 + 1 2 d x = 18 - 9 2 - 2 3 + 1 6

∫ 0 2 2 2 x x 2 + 1 - x x 2 + 1 2 d x = 13

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

A = 13

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1