UFMG, Sem Campus, Cálculo 3, P3 – 2022.1 – Questão 1
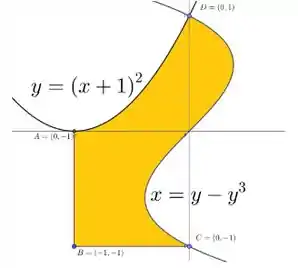
Observe a figura abaixo, a região hachurada é limitada pelas curvas e .
Escreva às integrais duplas necessárias para encontrar a área da região hachurada. Detalhe os pedaços de regiões utilizadas na sua decomposição.
Não é necessário calcular as integrais.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Para resolvermos o nosso exercício, vamos ter que dividir a nossa região em 2 partes:
Para começar, vamos esboçar as integrais da primeira parte (I). Se a gente analisar, vamos ter:
Show, agora vamos analisar a variação de . Reparem que a função está abaixo da , porém, precisamos colocar a primeira equação em função de :
Show, agora vamos ver que:
Logo o intervalor de integração vai ser:
Passo 2
Show, agora vamos para a segunda área
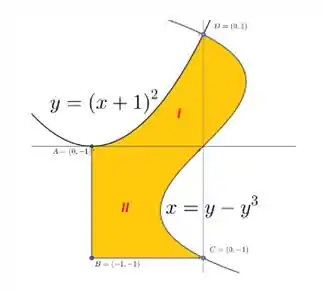
Vamos seguir a mesma ideia para esboçar as integrais da segunda parte (II). Se a gente analisar, vamos ter:
Show, agora vamos analisar a variação de . Reparem que temos uma reta abaixo da . Vamos ver que:
Logo o intervalor de integração vai ser:
Show, se somarmos, vamos ter: