Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 812345679101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1) Calcular a área da parte da superfície x 2 + y 2 + z 2 = 6 z que está dentro da região x 2 + y 2 ≤ z .

Passo 1

Bem, você precisa estar consciente de que, a essa altura do campeonato, área de superfície é dada por uma integral de superfície escalar:

A = ∬ S   1   d S

E como toda integral de superfície, temos um bom passo a passo a seguir até o fim da nossa jornada:

  1. Parametrizar a superfície S pedida no problema
  2. Encontrar o termo d S

E aí? Bora? :D

Passo 2

Precisamos parametrizar a superfície que queremos a área, mas por falar nisso, quem é essa superfície?

O próprio problema nos disse que ela é a parte dessa esfera x 2 + y 2 + z 2 = 6 z , que por falar nisso, não é uma esfera tão legal conosco afinal ela está deslocada:

x 2 + y 2 + z 2 = 6 z           →             x 2 + y 2 + z 2 - 6 z = 0

Completando quadrado... z - 3 2 - 9 = z 2 - 6 z , percebemos isso:

  x 2 + y 2 + z - 3 2 - 9 = 0     →

x 2 + y 2 + z - 3 2 = 3 2

Uma esfera de raio 3 , deslocada 3 unidades pra cima:

Mas, não queremos a esfera toda, e sim apenas a parte dentro do paraboloide z = x 2 + y 2 ...

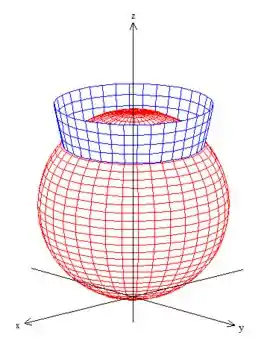
Eis a nossa superfície...

Passo 3

Ok, parametrizar um pedaço de uma esfera é bem parecido com a mudança para coordenadas esféricas:

x = R sin ⁡ φ cos ⁡ θ

y = R sin ⁡ φ sin ⁡ θ

z = R cos ⁡ φ

Com apenas dois detalhes:

1º - Aqui não tem esse R , pois se lembre de que superfície precisa apenas de dois parâmetros (2D). Então trocamos o R pelo raio da esfera:

x = 3 sin ⁡ φ cos ⁡ θ

y = 3 sin ⁡ φ sin ⁡ θ

z = 3 cos ⁡ φ

2º - Essa parametrização é para esferas centradas na origem. Se deslocamos a nossa 3 unidades para cima em z , então... A parametrização final é:

x = 3 sin ⁡ φ cos ⁡ θ

y = 3 sin ⁡ φ sin ⁡ θ

z = 3 cos ⁡ φ + 3

Viu só como é uma construção bem legal. Anotando essa parametrização de uma forma mais “matemática”...

σ φ ,   θ = 3 sin ⁡ φ cos ⁡ θ ,   3 sin ⁡ φ sin ⁡ θ ,   3 cos ⁡ φ + 3

Passo 4

Sim, nunca saímos de uma parametrização sem antes determinar os limites dos parâmetros, no caso... φ e θ .

Quando realizamos a parametrização levando em consideração o deslocamento da esfera, z = 3 cos ⁡ φ + 3 , geometricamente é como se tivéssemos arrastado os eixos coordenados para o centro da esfera:

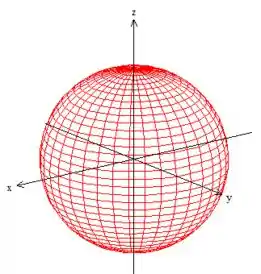
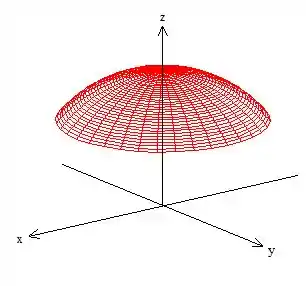
Bem e aqui, as coordenadas variam como as coordenadas esféricas normais, ou seja, o θ varia no plano x y , por isso fazemos uma projeção da superfície nele para sabermos a variação de θ :

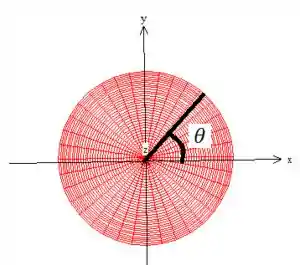
E repare que ele dá uma volta completa, por isso...

0 ≤ θ ≤ 2 π

Passo 5

Quanto ao φ , ele varia do eixo z e vai descendo até a borda:

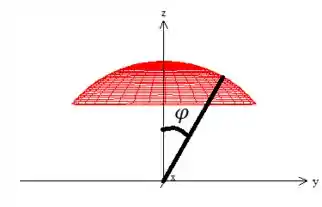
Como pode ver, φ sai do 0 e vai até a borda, ou seja onde a esfera é delimitada pelo paraboloide. Fazer essa delimitação em matemática é justamente encontrar a solução do sistema com as duas equações:

x 2 + y 2 + z 2 = 6 z x 2 + y 2 = z     →

x 2 + y 2 + z 2 = 6 z       →           z + z 2 = 6 z       →

z 2 = 5 z         →             z = 5

Então elas se encontram em z = 5 . Substituindo a parametrização:

z = 3 cos ⁡ φ + 3         →           3 cos ⁡ φ + 3 = 5

3 cos ⁡ φ = 2         →           cos ⁡ φ = 2 3

Então, o limite do ângulo φ é um cara, vamos chamar φ 0 , que satisfaz cos ⁡ φ 0 = 2 3 . Não o conhecemos, mas não é algo muito relevante. O que é importante é saber que então...

0 ≤ φ ≤ φ 0

Passo 6

Muito bem, parametrização dada como concluída, podemos buscar o termo d S :

d S = N → d φ d θ

Onde esse vetor norma N → ...

N → = ∂ σ ∂ φ × ∂ σ ∂ θ

Como σ φ ,   θ = 3 sin ⁡ φ cos ⁡ θ ,   3 sin ⁡ φ sin ⁡ θ ,   3 cos ⁡ φ + 3 , podemos calcular essas derivadas parciais:

∂ σ ∂ φ = 3 cos ⁡ φ cos ⁡ θ , 3 cos ⁡ φ sin ⁡ �� , - 3 sin ⁡ φ

∂ σ ∂ θ = - 3 sin ⁡ φ sin ⁡ θ ,   3 sin ⁡ φ cos ⁡ θ ,   0

Um produto vetorial é dado pelo determinando dos vetores calculados...

N → = ∂ σ ∂ φ × ∂ σ ∂ θ

N → = i → j → k → 3 cos ⁡ φ cos ⁡ θ 3 cos ⁡ φ sin ⁡ θ - 3 sin ⁡ φ - 3 sin ⁡ φ sin ⁡ θ 3 sin ⁡ φ cos ⁡ θ 0

Com paciência, resolvendo esse determinante 3 × 3 ...

N → = 9 sin 2 ⁡ φ sin ⁡ θ j → + 9 cos ⁡ φ sin ⁡ φ cos 2 ⁡ θ k → - - 9 sin 2 ⁡ φ cos ⁡ θ i → - 9 cos ⁡ φ sin ⁡ φ sin 2 ⁡ θ k →

N → = 9 sin 2 ⁡ φ sin ⁡ θ j → + 9 cos ⁡ φ sin ⁡ φ cos 2 ⁡ θ k → + 9 sin 2 ⁡ φ cos ⁡ θ i → + 9 cos ⁡ φ sin ⁡ φ sin 2 ⁡ θ k →

Colocando em evidência a parte do k → ...

N → = 9 sin 2 ⁡ φ cos ⁡ θ i → + 9 sin 2 ⁡ φ sin ⁡ θ j → + 9 cos ⁡ φ sin ⁡ φ sin 2 ⁡ θ + cos 2 ⁡ θ k →

N → = 9 sin 2 ⁡ φ cos ⁡ θ i → + 9 sin 2 ⁡ φ sin ⁡ θ j → + 9 cos ⁡ φ sin ⁡ φ k →

Logo, o vetor normal é...

N → = 9 sin 2 ⁡ φ cos ⁡ θ ,   9 sin 2 ⁡ φ sin ⁡ θ , 9 cos ⁡ φ sin ⁡ φ  

Passo 7

Toda superfície tem dois vetores normais: esse e a versão negativa dele. Para nós, isso não interessa, pois queremos o módulo:

N → = 9 sin 2 ⁡ φ cos 2 ⁡ θ 2 + 9 sin 2 ⁡ φ sin 2 ⁡ θ 2 + 9 cos ⁡ φ sin ⁡ θ 2

N → = 9 2 sin 4 ⁡ φ cos 2 ⁡ θ + 9 2 sin 4 ⁡ φ sin 2 ⁡ θ + 9 2 cos 2 ⁡ φ sin 2 ⁡ φ

N → = 9 2 sin 4 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ + 9 2 cos 2 ⁡ φ sin 2 ⁡ φ =

N → = 9 2 sin 4 ⁡ φ + 9 2 cos 2 ⁡ φ sin 2 ⁡ φ

N → = 9 2 sin 2 ⁡ φ sin 2 ⁡ φ + cos 2 ⁡ φ

N → = 9 2 sin 2 ⁡ φ

Como estamos trabalhando com um φ entre 0 e 90 ° , o seno é positivo ...

N → = 9 sin ⁡ φ

Logo:

d S = 9 sin ⁡ φ   d φ d θ

Passo 8

Finalmente regressando à integral que iremos resolver para obter a área:

A = ∬ S   1   d S

e substituindo S pelas variações

0 ≤ θ ≤ 2 π

0 ≤ φ ≤ φ 0

e o d S ...

A = ∫ 0 2 π ∫ 0 φ 0 9 sin ⁡ φ d φ d θ

Agora é só calcular e ser feliz :D

A = 9 ∫ 0 2 π ∫ 0 φ 0 sin ⁡ φ   d φ d θ

A = 9 ∫ 0 2 π - cos ⁡ φ 0 φ 0 d θ

A = 9 ∫ 0 2 π - cos ⁡ φ 0 - - cos ⁡ 0   d θ

Epa! Olha que legal, apareceu cos ⁡ φ 0 e sabemos que cos ⁡ φ 0 = 2 3 ...

A = 9 ∫ 0 2 π - 2 3 + 1   d θ

A = 9 1 3 ∫ 0 2 π   d θ

A = 3 2 π = 6 π

Resposta

6 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1