Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 104123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Calcule a massa da superfície S de equação

x 2 + y 2 + z - 2 2 = 1

E densidade γ x ,   y ,   z = 1 x 2 + y 2 + z 2 , com x 2 + y 2 + z 2 ≠ 0 .

Passo 1

Bem, uma massa de um pedaço de superfície S é nos dado agora por uma integral de superfície caso escalar e sua cara é...

M S = ∬ S   γ x ,   y ,   z   d S

Como estamos trabalhando com uma integral de superfície, podemos muito bem utilizar o passo a passo maroto para detonar o problema imposto:

  1. 1º - Parametrizar a superfície S .
  2. 2º - Substituir os termos da parametrização na função γ ( x ,   y ,   z ) .
  3. 3º - Encontrar o termo d S .

Passo 2

Vamos começar com o primeiro, onde no caso vamos parametrizar S . Por falar nisso, quem é a superfície? Para termos uma noção do que fazermos, recomendo fortemente que desenhe a superfície...

No caso, estamos trabalhando com uma esfera deslocada em duas unidades no eixo z , mas que tem um raio 1 ...

x 2 + y 2 + z - 2 2 = 1

Passo 3

A gente pode parametrizar uma esfera sempre utilizando as equações da mudança para coordenadas esférica:

x = R sin ⁡ φ cos ⁡ θ

y = R sin ⁡ φ sin ⁡ θ

z = R cos ⁡ φ

A diferença é que agora estamos trabalhando com uma superfície esférica, e como toda superfície, apenas precisamos de dois parâmetros para descrever os seus pontos no espaço. No caso da esfera, esse R é o raio da esfera que no caso vale 1 ...

x = sin ⁡ φ cos ⁡ θ

y = sin ⁡ φ sin ⁡ θ

z = cos ⁡ φ

Outra curiosidade que não podemos esquecer é que a nossa esfera está deslocada 2 unidades em z ( x 2 + y 2 + z - 2 2 = 1 ). Então devemos levar isso em consideração:

x = sin ⁡ φ cos ⁡ θ

y = sin ⁡ φ sin ⁡ θ

z = cos ⁡ φ + 2

Concluímos então que uma boa parametrização para essa esfera S é essa daqui:

σ θ ,   φ = sin ⁡ φ cos ⁡ θ ,   sin ⁡ φ sin ⁡ θ ,   cos ⁡ φ + 2

Passo 4

Como toda parametrização, precisamos definir onde os parâmetros variam. No caso dessa parametrização, os parâmetros são φ e θ e, como já comentamos, esses caras tem origem nas coordenadas esféricas e eles sempre variam dessa forma aqui:

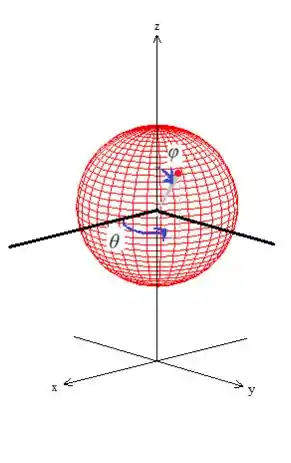
Veja então que para formarmos essa esfera, a gente tem um θ dando um giro de 360   graus...

0 ≤ θ ≤ 2 π

Enquanto temos o φ dando uma volta de 180 ° ...

0 ≤ φ ≤ π

Passo 5

Concluída esta etapa, encontremos a função γ x ,   y ,   z que estamos integrando em termos dos parâmetros:

  γ x ,   y ,   z = 1 x 2 + y 2 + z 2

Substituindo os termos da parametrização, onde para se recordar:

x = sin ⁡ φ cos ⁡ θ y = sin ⁡ φ sin ⁡ θ z = cos ⁡ φ + 2

Então...

  γ σ θ ,   φ = 1 sin ⁡ φ cos ⁡ θ 2 + sin ⁡ φ sin ⁡ θ 2 + cos ⁡ φ + 2 2       →

Simplificando isso tudo vamos ganhar...

  γ σ θ ,   φ = 1 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ φ sin 2 ⁡ θ + cos 2 ⁡ φ + 4 cos ⁡ φ + 4       →

γ σ θ ,   φ = 1 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ + cos 2 ⁡ φ + 4 cos ⁡ φ + 4       →

γ σ θ ,   φ = 1 sin 2 ⁡ φ + cos 2 ⁡ φ + 4 cos ⁡ φ + 4       →

γ σ θ ,   φ = 1 1 + 4 cos ⁡ φ + 4       →

γ σ θ ,   φ = 1 4 cos ⁡ φ + 5

Passo 6

Beleza, então podemos sair em busca do termo d S ...

d S = N →   d φ d θ

Onde esse vetor normal é dado por...

N → = ∂ σ θ , φ ∂ θ × ∂ σ θ , φ ∂ φ

Porém, como estamos trabalhando com uma parametrização bem conhecida, a parametrização de uma esfera deslocada da origem, podemos memorizar esse módulo do vetor normal aí, afinal ele é bem parecido com o Jacobiano lá nas coordenadas esféricas:

N → = R 2 sin ⁡ φ

A diferença é que aqui o nosso raio R é conhecido ( R = 1 ) ...

N → = 1 2 sin ⁡ φ   →

N → = sin ⁡ φ

Então

d S = sin ⁡ φ   d φ d θ

Passo 7

Voltando para a integral que buscamos a solução...

M S = ∬ S   γ x ,   y ,   z   d S =

∫ 0 2 π ∫ 0 π 1 4 cos ⁡ φ + 5 ⋅ sin ⁡ φ d φ d θ

Agora é só calcular essa integral aí mesmo. Por falar nisso, vamos começar com a de dentro:

∫ 0 2 π ∫ 0 π sin ⁡ φ 4 cos ⁡ φ + 5 d φ d θ =

Fazendo uma mudança...

4 cos ⁡ φ + 5 = u           →                     d u = - 4 sin ⁡ φ d φ           o u

sin ⁡ φ d φ = - d u 4

Trocando também os limites de integração...

φ = 0                   →                   u =   4 cos ⁡ 0 + 5 = 9

φ = π                   →                   u =   4 cos ⁡ π + 5 = 1

Então...

∫ 0 2 π ∫ 0 π sin ⁡ φ 4 cos ⁡ φ + 5 d φ d θ = ∫ 0 2 π ∫ 9 1 1 u - d u 4 d θ =

1 4 ∫ 0 2 π ∫ 1 9 1 u d u d θ = 1 4 ∫ 0 2 π 2 u 1 9 d θ =

1 4 ∫ 0 2 π 2 9 - 2 1 d θ = 1 4 ∫ 0 2 π 6 - 2 d θ =

4 4 ∫ 0 2 π d θ = 2 π

Resposta

2 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1