Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 120123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Seja a superfície parametrizada

r t ,   θ = t 2 2 cos ⁡ θ , t 2 2 sin ⁡ θ ,   t ,     - 2 ≤ t ≤ 0

  1. Calcule a equação cartesiana da imagem de   r .
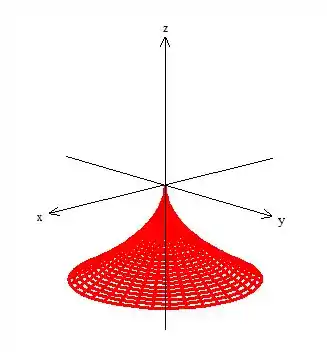
  2. Faça um esboço da imagem de r .
  3. Justifique se a imagem de r é uma superfície regular ou não.
  4. Calcule a equação implícita do plano tangente no ponto r - 1 , π 2 .
  5. Calcule ∬ r   48 x 2 + y 2 z 5 d S

Passo 1

a )

Bem, para resolver esse item, devemos lembrar que na equação paramétrica, cada entrada do vetor representa uma coordenada cartesiana:

r t ,   θ = t 2 2 cos ⁡ θ ⏟ x , t 2 2 sin ⁡ θ ⏟ y ,   t ⏟ z

Ou seja:

x = t 2 2 cos ⁡ θ

y = t 2 2 sin ⁡ θ

z = t

Lembrando que cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ...

x 2 + y 2 = t 2 2 cos ⁡ θ 2 + t 2 2 sin ⁡ θ 2 =

t 4 4 cos 2 ⁡ θ + t 4 4 sin 2 ⁡ θ =

t 4 4 cos 2 ⁡ θ + sin 2 ⁡ θ =

t 4 4

Viu só? Com essa técnica a gente elimina o θ da parada, logo ficamos com...

x 2 + y 2 = t 4 4

Como z = t ... Ganhamos a equação cartesiana da superfície:

x 2 + y 2 = z 4 4

Passo 2

b )

Aqui queremos desenhar a superfície que acabamos de encontrar. Para fazer isso, primeiro vamos desenhar no espaço, a intersecção da superfície com os planos z y e z x para termos uma ideia de quem é a superfície:

Para a intersecção com o plano z y , fazemos x = 0 ...

x 2 + y 2 = z 4 4           →             y 2 = z 4 4             →

y = z 2 2

Esse cara é uma parábola:

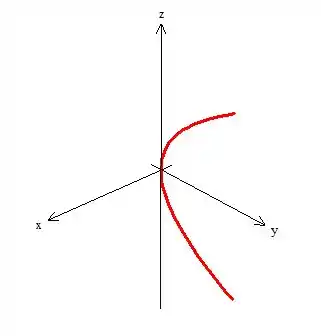
Para a intersecção com z x , devemos colocar y = 0 ...

x 2 + y 2 = z 4 4           →             x 2 = z 4 4             →

x = z 2 2

OPA! Encontramos a mesma parábola, mas agora no plano z x :

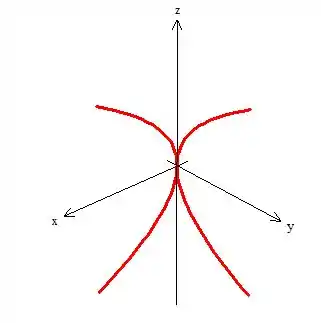
Isso sugere que a nossa superfície é uma superfície de revolução, veja:

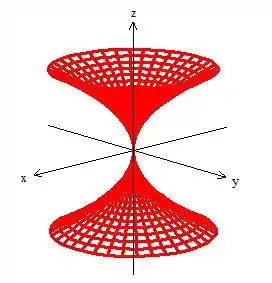
Só tem mais um detalhe: queremos a superfície limitada com - 2 ≤ t ≤ 0 , como t = z ... - 2 ≤ z ≤ 0 , o que significa que queremos apenas um pedacinho da superfície delimitada em z dessa forma:

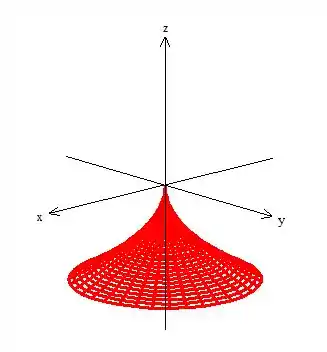
E essa é a nossa superfície !

Passo 3

c )

OK! Como vamos fazer tal verificação pedida aqui??

CALMA! Veja só, a gente vai segui a teoria para verificar, ou seja, primeiro, vamos passar esse z 4 / 4 pro outro lado:

x 2 + y 2 = z 4 4           →               x 2 + y 2 - z 4 4 = 0

E vamos considerar que a nossa superfície é a superfície de nível 0 da função g x ,   y ,   z onde

g x ,   y ,   z = x 2 + y 2 - z 4 4

Pela definição, devemos verificar, para verificar se a superfície é ou não regular, devemos calcular o gradiente de tal função:

∇ g x ,   y ,   z = ∂ g ∂ x , ∂ g ∂ y , ∂ g ∂ z = 2 x ,   2 y ,   - z 3

Como existe um ponto pertencente à superfície que 0 esse gradiente:

∇ g 0 ,   0 ,   0 = 0 ,   0 ,   0

Concluímos que essa descrição da imagem da superfície, em coordenadas cartesianas, não é regular!

Passo 4

d )

Pela equação de plano tangente temos:

x - x 0 ,   y - y 0 ,   z - z 0 ⋅ ∇ g x 0 ,   y 0 ,   z 0 = 0

Onde ( x 0 ,   y 0 ,   z 0 ) é o pronto de tangencia definido pra gente como sendo o ponto onde:

r - 1 , π 2 = - 1 2 2 cos ⁡ π 2 , - 1 2 2 sin ⁡ π 2 ,   - 1 =

0 , 1 2 ⋅ 1 ,   - 1 =

0 , 1 2 ,   - 1

Logo...

x ,   y - 1 2 ,   z + 1 ⋅ ∇ g 0 , 1 2 ,   - 1 = 0

Como...

∇ g x ,   y ,   z = 2 x ,   2 y ,   - z 3       →

∇ g 0 , 1 2 ,   - 1 = 2 0 ,   2 1 2 ,   - - 1 3       →

∇ g 0 , 1 2 ,   - 1 = 0 ,   1 ,   1

Portanto, a equação do plano tangente nesse ponto é:

x ,   y - 1 2 ,   z + 1 ⋅ 0 ,   1 ,   1 = 0       →

y - 1 2 ⋅ 1 + z + 1 ⋅ 1 = 0   →

y - 1 2 + z + 1 = 0   →

y + z = - 1 2

Passo 5

e )

Por último devemos calcular a integral de superfície:

∬ r   48 x 2 + y 2 z 5 d S

Como toda integral de superfície, vamos encontrar a integral de superfície escalar seguindo o método:

  1. Parametrizar a superfície S .
  2. Encontrar o termo d S .
  3. Substituir os termos da parametrização na função.

Passo 6

O primeiro passo da resolução está concluído, pois a superfície já nos foi dada parametrizada:

r t ,   θ = t 2 2 cos ⁡ θ , t 2 2 sin ⁡ θ ,   t ,     - 2 ≤ t ≤ 0

Veja que como a superfície dá uma volta completa ao redor de z , podemos afirmar que:

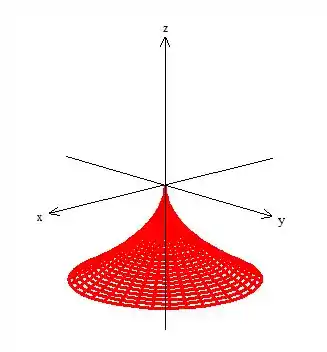
E isso implica...

0 ≤ θ ≤ 2 π

Passo 7

O segundo passo, nos manda encontrar o termo d S ...

d S = N → d t d θ

Onde

N → = ∂ r ∂ t × ∂ r ∂ θ  

Como

∂ r ∂ t = t cos ⁡ θ ,   t sin ⁡ θ ,   1

∂ r ∂ θ = - t 2 2 sin ⁡ θ , t 2 2 cos ⁡ θ ,   0

Logo...

N → = ∂ r ∂ t × ∂ r ∂ θ = i ^ j ^ k ^ t cos ⁡ θ t sin ⁡ θ 1 - t 2 2 sin ⁡ θ t 2 2 cos ⁡ θ 0 =

- t 2 2 sin ⁡ θ j ^ + t 3 2 cos 2 ⁡ θ k ^ - t 2 2 cos ⁡ θ i ^ + t 3 2 sin 2 ⁡ θ k ^ =

- t 2 2 cos ⁡ θ i ^ - t 2 2 sin ⁡ θ j ^ + t 3 2 sin 2 ⁡ θ + t 3 2 cos 2 ⁡ θ k ^ =

- t 2 2 cos ⁡ θ i ^ - t 2 2 sin ⁡ θ j ^ + t 3 2 k ^

Ou...

N → = - t 2 2 cos ⁡ θ ,   - t 2 2 sin ⁡ θ ,   t 3 2

Para calcular o módulo...

N → = - t 2 2 cos ⁡ θ 2 + - t 2 2 sin ⁡ θ 2 + t 3 2 2       →

N → = t 4 4 cos 2 ⁡ θ + t 4 4 sin 2 ⁡ θ + t 6 4       →

N → = t 4 4 + t 6 4       →

N → = t 4 4 1 + t 2       →

N → = t 2 2 1 + t 2    

Logo...

d S = t 2 2 1 + t 2 d t d θ

Passo 8

A terceira e última coisa que devemos fazer antes de retornar para a integral é substituir a parametrização na função que estamos integrando:

48 x 2 + y 2 z 5 =

Como vimos no passo 1 ...

48 t 4 4 t 5 =

12 t

Passo 9

Voltando para a integral e substituindo...

∬ r   48 x 2 + y 2 z 5 d S = ∫ 0 2 π ∫ - 2 0 12 t ⋅ t 2 2 1 + t 2   d t d θ =

∫ 0 2 π ∫ - 2 0 6 t 1 + t 2   d t d θ

Fazendo uma substituição do tipo...

1 + t 2 = u         →

d u = 2 t   d t

Trocando também os limites de integração...

t = - 2                       →                   u = 1 + - 2 2 = 5

t = 0                       →                   u = 1 + 0 2 = 1

∫ 0 2 π ∫ 5 1 3 u   d u d θ = ∫ 0 2 π 3 2 3 u 3 2 5 1 d θ =

∫ 0 2 π 3 2 3 - 2 3 5 3 2 d θ =

Como 5 3 / 2 = 5 5

∫ 0 2 π 3 2 - 10 5 3 d θ = 2 - 10 5 2 π =

4 π - 2 0 π 5

Resposta

a )   x 2 + y 2 = z 4 4

b )

c )   N ã o   é   r e g u l a r

d )   y + z = - 1 2

e )   4 π - 2 0 π 5

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1