Seja a parte da superfície com e , limitada pelos planos e . Então, o valor de é:
a)
b)
c)
d)
e)
Passo 1
Vamos lá! Tem um passo a passo para gente calcular essa integral de superfície escalar. Só seguir ele, que dá bom!
A gente vê que nossa superfície é uma curva , em , transladada na direção de e que forma uma espécie de cilindro, tudo bem? Assim oh:
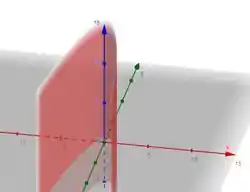
Então vamos começar parametrizando essa curva em . Podemos usar a parametrização natural assim:
Nosso parâmetro pode ser o próprio , e a nossa parametrização dessa curva fica:
Mas precisamos que o domínio dessa curva atenda a dois critérios:
E
Desse modo, o domínio desse parâmetro é:
Mas lembra que a gente quer parametrizar uma superfície. Então precisamos de dois parâmetros. Como nossa curva só translada de e no eixo para formar nosso cilindro, podemos dizer que a componente é o próprio , nosso segundo parâmetro.
E fazer algo assim:
Com:
Passo 2
Agora a gente calcula o vetor normal a nossa superfície:
E como a integral é escalar, a gente precisa tirar o módulo desse cara:
Passo 3
Para que fizemos tudo isso? Cara, para montar nossa integral:
Para a gente:
E como na parametrização, a componente é o próprio . Quando a gente substitui a nossa parametrização nessa , ela nem muda:
E o domínio é o domínio da parametrização:
Aí a integral fica:
Passo 4
Calculando essa belezura:
Vamos usar uma substituição simples na integral de dentro:
Os novos extremos de integração ficam:
E a integral mudada é:
Resposta
Letra d