Seja o pedaço do cone acima do cilindro e embaixo do cilindro . Calcule a área da superfície S.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão foi dito que temos um solido que está dentro do cone descrito por acima de um cilindro descrito por e abaixo de outro cilindro descrito por .
Com base nesse sólido, temos que descobrir a área da sua superfície.
E aí! Como podemos fazer para obter essa área? 👀
A gente até consegue calcular uma área sem vê-la, mas você concorda que fica muito mais difícil? já que não temos alguns parâmetros mentais para ajudar a gente.
Dessa forma podemos começar esboçando as curvas que limitam nosso objeto.
A equação descreve um cilindro deitado no eixo , a equação descreve um cilindro deitado no eixo e a equação descreve um cone de cabeça para baixo.
Esboçando essas equações em

É um negocio muito louco, não é? 👀
Passo 2
Perceba que nesse sólido queremos apenas a superfície azul limitada pelos cilindros verde e amarelo.
Lembrando lá de integrais de superfícies, em um caso escalar, quando temos que obter a área de uma superfície temos de calcular
Onde o obtido por um vetor normal à superfície
Nesse ponto, o segredo é parametrizar a superfície que queremos e calcular um vetor normal a essa superfície.
Já são os limites de integração que vamos obter na projeção da superfície no plano .
Entendeu? Bora começar!
No caso escalar onde é explicito na função, o vetor normal é obtido a partir do gradiente
Calculando a derivada parcial de com relação a , temos que aplicar a regra da cadeia já que é uma função composta.
Lembrando que a regra da cadeia é dada pela derivada de dentro multiplicada pela derivada de fora.
Substituindo por na derivada de fora, vamos chegar em
Pelo método de derivação polinomial, temos
Substituindo por de volta, chegamos em
Tranquilo até aqui? 👀
Passo 3
Agora vamos calcular a derivada de com relação a .
Perceba que vamos usar os mesmo métodos, porem agora com relação a .
Derivando pela regra da cadeia...
Pelo método de derivação polinomial, temos
Substituindo por de volta, chegamos em
E rapidinho, por último, derivando com relação a ...
Dessa forma, nosso vetor normal fica como
Interessante, não é? 🤩
Passo 4
E agora, nos resta calcular o modulo desse vetor.
Dado um vetor , seu módulo é calculado como , portanto
Como , então
E também quando temos , logo
Simplificando...
Com isso, dado que , nossa integral fica
Perceba que é a área projetada no plano da superfície que estamos interessados.
Bora ver que região é essa?
Passo 5
Então vamos eliminar dos limites de .
O limite inferior é dado pelo cilindro se substituirmos a nossa superfície nessa equação, temos
Essa equação é familiar para a gente, não é?
Onde e
Se fizermos o mesmo para o limite superior de , onde o cilindro é dado pela equação . Substituindo nossa superfície nessa equação, temos
Essa equação também é muito parecida com a equação de uma elipse, organizando esse resultado, temos
Se esboçarmos os gráficos no plano , podemos visualizar a região que queremos integrar.
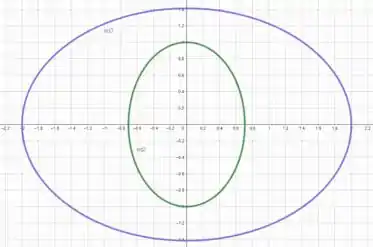
A curva verde representa o limite inferior de e a curva roxa representa o limite superior de .
Como uma elipse está em pé e a outra está deitada, seria muito difícil definir os limites de integração em uma integral só.
Mas você concorda que a área que estamos integrando é a área limitada pela curva roxa menos a área limitada pela curva verde?
Então podemos calcular a área maior e subtrair da área menor, não é?
Entendeu? 👀
Passo 6
Como a integral da área de uma superfície é
Se e a área de uma elipse é dada por , ou seja
é representada pela equação , onde e .
Já é representada pela equação , onde e .
Com isso
Logo...
Substituindo essa informação em , vamos finalmente obter a área da nossa superfície.
Como
Chegamos ao fim! A área da nossa superfície limitada por aquelas regiões bem estranhas é igual a !
Fim! Iae, o que achou? Responde Aí! 😁
