Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 112123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Áreas de superfícies

Seja S a superfície do cilindro x 2 + y 2 = 4 com 0 ≤ z ≤ 4 - x 2 4 + y 2 , e contida no semi espaço y ≥ 0 . Calcule a área de S .

Passo 1

Vamos, antes de tudo, desenhar essa superfície para termos uma ideia melhor do problema. Temos um cilindro de raio 2 centrado na origem, cortado pelo plano z = 0 e pelo paraboloide z = 4 - x 2 4 + y 2 :

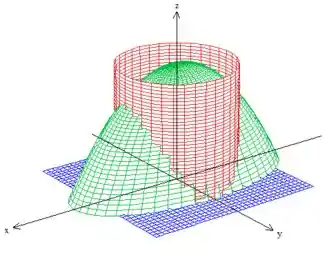
Então, S é a parte do cilindro que está entre o paraboloide e o plano e tem y ≥ 0 .

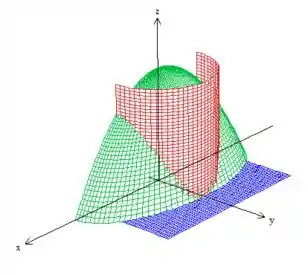
S é a parte do cilindo vermelho que está abaixo do paraboloide verde, que não conseguimos ver. Para você entender melhor, vamos olhar por trás dessa figura:

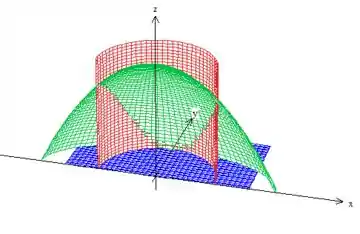
Vamos usar essa fórmula aqui para calcular a área da superfície:

A S = ∬ D   ∂ φ ∂ u × ∂ φ ∂ v d u d v

Passo 2

Agora precisamos parametrizar a superfície. Como se trata de um cilindro, vamos usar coordenadas cilíndricas com r = 2 :

x = 2 cos ⁡ θ

y = 2   s e n   θ

z = z

Isso nos dá:

φ θ , z = 2 cos ⁡ θ , 2   s e n   θ , z

Como temos meia volta em torno do eixo z , 0 ≤ θ ≤ π (lembra que a superfície é limitada a y ≥ 0 ). O intervalo de z vai desde z = 0 (no plano) até onde o cilindro encontra o paraboloide, então, vamos substituir a parametrização do cilindro na equação do paraboloide:

z = 4 - 2 cos ⁡ θ 2 4 + 2   s e n   θ 2

z = 4 - cos 2 ⁡ θ - 4 s e n 2 θ

z = 4 - 1 - 3 s e n 2 θ

z = 3 - 3 s e n 2 θ

Então 0 ≤ z ≤ 3 - 3 s e n 2 θ , show?

Passo 3

Calcular ∂ φ ∂ θ e ∂ φ ∂ z

∂ φ ∂ θ = ( - 2 s e n   θ ,   2 cos ⁡ θ , 0 )

∂ φ ∂ z = ( 0,0 , 1 )

Passo 4

Calcular N → θ , z

N → θ , z = ∂ φ ∂ θ × ∂ φ ∂ z

N → θ , z = i j k - 2 s e n   θ 2 cos ⁡ θ 0 0 0 1

N → θ , z = ( 2 cos ⁡ θ , 2   s e n   θ , 0 )

N → θ , z = ( 2 cos ⁡ θ ) 2 + ( 2   s e n   θ ) 2 + 0

N → θ , z = 2

Passo 5

Agora vamos montar a integral

A S = ∬ D   2 d z θ

Onde D é dado por:

0 ≤ θ ≤ π

0 ≤ z ≤ 3 - 3 s e n 2 θ

A S = ∫ 0 π ∫ 0 3 - 3 s e n 2 θ 2 d z d θ

Passo 6

Agora isso aí virou questão de integral dupla, né? Bora resolver isso aí:

A S = 2 ∫ 0 π z 0 3 - 3 s e n 2 θ d θ

= 6 ∫ 0 π 1 - s e n 2 θ d θ =

Leambrando que:

s e n 2 θ = 1 - c o s ⁡ ( 2 θ ) 2

Temos

= 6 ∫ 0 π 1 - 1 - c o s ⁡ ( 2 θ ) 2 d θ =

= 6 ∫ 0 π 1 2 + c o s ⁡ ( 2 θ ) 2 d θ =

= 3 ∫ 0 π 1 + c o s ⁡ ( 2 θ ) d θ =

= 3 θ + 1 2 s e n 2 θ 0 π =

= 3 π + 0 - 0 + 0 = 3 π

Resposta

3 π

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1