UTFPR, Londrina, Cálculo 3, Provas de C3 - Prof Marcele Tavares - AV1 - 2023.1, Questão 4.i
Suponha:
- Uma superfície S dada por
- é a intersecção de S com
- é a intersecção de S com
Escolha um dos campos vetoriais para a partir de S, γ1 e γ2 elaborar:
i. um exercício que envolva o cálculo de Trabalho.
Passo 1
Olá meu amigo, espero que continue me achando um amigo depois da questão que preparei para resolvermos hehe. Essa questão é extremamente pessoal, então fique a vontade para olhar nos livros algumas questões sobre Fluxo e apenas mudar a Superfície S, mas eu utilizei um pouco da minha criatividade e trouxe aqui uma para resolvermos juntos.
Primeiro vamos analisar a nossa superfície S.
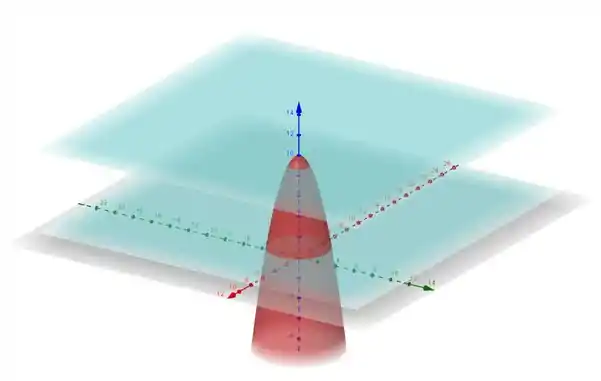
S é a superfície vermelha que está entre esses 2 planos azuis. É tipo um chapéu de aniversario porem cortado na ponta e ali se colocou um papel plano.
Passo 2
O exercício que iremos criar é o seguinte:
Considere o campo vetorial e a superfície S dada por , onde . Calcule o trabalho realizado pelo campo F ao mover uma partícula ao longo da curva , que é a intersecção da superfície S com o plano , no sentido anti-horario, de para .
Agora é a hora de resolver,
A curva é dada por , então substituímos por 1 nas componentes de F:
A parametrização da curva pode ser dada por onde , e . Onde o intervalo de é
O trabalho de é dado por:
Hehe, peguei leve com você, um forte abraço e até uma próxima.
Resposta
Ver o desenvolvimento.