Associe cada figura com sua equação polar

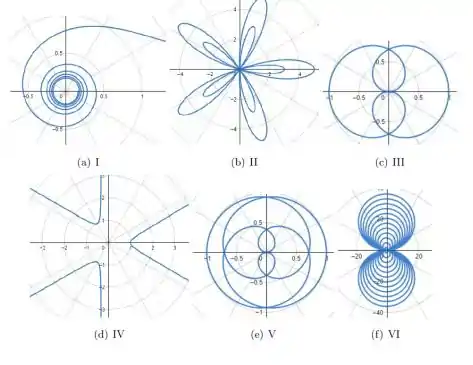
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Calc 2. Nosso objetivo é associar cada figura com a equação polar dada.

Passo 2
Vamos começar analisando a curva
Note que para valores de próximo de zero, o raio da nossa curva vai para infinito, e conforme aumentamos , o raio da curva vai diminuindo até chegar em zero. Como a única curva que tem esse comportamento é a curva desenhada . Temos nossa primeira relação
Agora, vamos analisar a curva
Note que essa curva apresenta uma simetria para os valores de . Ela tem um período de . analisando o crescimento do ângulo , vemos que nosso raio assume os seguintes valores
Quando
Quando
Quando
Quando
Quando
Agora, analisando de , vemos que teremos os mesmos valores, mas com sinais trocados.
Logo,nossa curva será dada por
De modo análogo a curva anterior, temos que
Agora, vamos analisar a curva
Note que para valores de da forma nosso denominador se aproxima de zero, e o valor do raio explode, e o valor mínimo do nosso raio é .
Como a única curva que tem esse comportamento é a curva desenhada . Temos nossa primeira relação
Passo 3
Agora, vamos analisar a curva
Nosso raio vai crescendo em função de , contudo, temos uma mudança de sinal do nosso raio quando saímos dos intervalos e vamos para os intervalos intervalos
Ou seja, nossa curva vai crescendo indefinidamente ao redor da origem (sempre retornando para a origem).
omo a única curva que tem esse comportamento é a curva desenhada . Temos nossa primeira relação
Só sobrou a curva

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊