UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 13, Questão 16
Faça o gráfico das funções . Determine o domínio, a imagem, o período e a paridade de cada uma delas.
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é Faça o gráfico das funções
Vale lembrar que
Então, vamos começar fazendo os gráficos mais simples,
Essas são as funções mais simples, e seus gráficos estão abaixo, respectivamente.
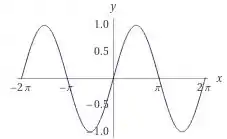
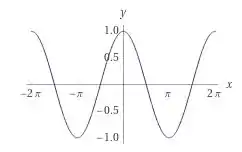
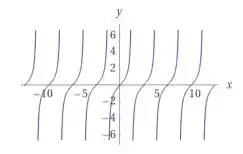
Olhando os gráficos, podemos observar que o é uma função ímpar ,que o é uma função par, e a é uma função ímpar
Quanto aos seus domínios. O estão bem definidos nos reais. Já a tangente, tem descontinuidades em
Passo 2
Agora, vamos para as funções . Seus gráficos estão abaixo, respectivamente.
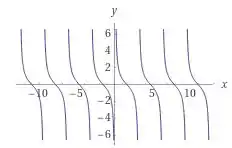
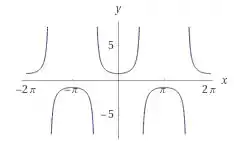
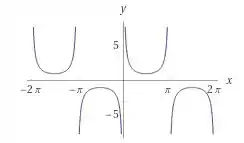
Olhando os gráficos, podemos observar que o é uma função ímpar ,que o é uma função par, e a é uma função ímpar
Quanto aos seus domínios. O tem descontinuidades em , a tem descontinuidades em , tem descontinuidades em
Ufaa!!!
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima