Seja a curva parametrizada:
Faça um esboço da trajetória percorrida pela partícula.
Passo 1
Identificar curva:
Pelas equações paramétricas da curva, podemos ver que
Logo:
Então essa é uma helicoidal cônica.
Passo 2
Avaliar :
Logo, a curva “sobe” com o aumento do parâmetro
Passo 3
Verificar intervalo e ponto inicial:
Como t é real, ele varia de a . Quando , a curva passa pelo ponto:
Passo 4
Esboçar curva:
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
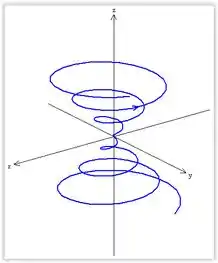
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica