UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 28
Faça os gráficos das funções abaixo
- .
- .
- .
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é desenhar os gráficos das funções logarítmicas.
Para isso, vamos aprender alguns macetes. Suponha que sabemos desenhar o gráfico de uma função . Então o gráfico de é o gráfico da refletido com relação ao eixo .
o gráfico de é o gráfico da refletido com relação ao eixo .
o gráfico de é o gráfico da transladado unidades para a direita se ou para a esquerda se .
Com isso em mente, vamos fazer os nossos gráficos
Vamos começar pela letra .
é o gráfico do log na base transladado
Vamos para a letra
é o gráfico do log refletido no eixo
Vamos para a letra .
é o gráfico do log na base refletido no eixo
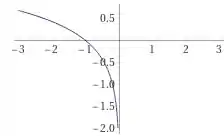
Vamos para a letra
é o gráfico do log natural transladado
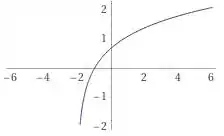
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima