UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 5a
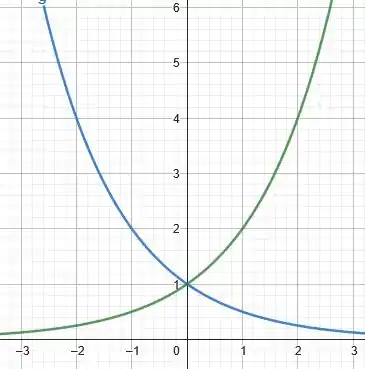
Em cada item, faça o gráfico das funções em um mesmo plano.
e
Passo 1
Eaí pessoaaaal, tudo numa boa com vocês??
Então, nesse exercício precisamos desenhar o gráfico de duas funções em um mesmo plano
Para isso, vamos montar uma pequena tabela com alguns valores de e os respectivos valores de e . Assim, podemos esboçar as curvas, beleza?!
Vamo nessa!
Passo 2
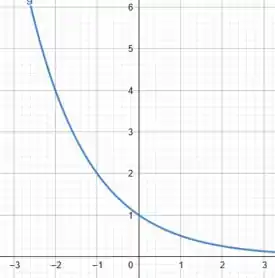
Começando pela função , podemos montar a seguinte tabela:
Daí, lembrando que é uma função exponencial, logo sua curva é uma hipérbole.
Podemos então plotar os pontos do gráfico em uma tabela e desenhar a curva:
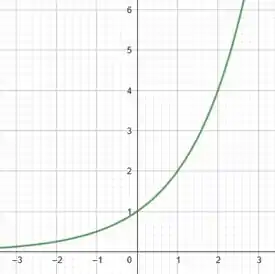
Passo 3
Fazendo o procedimento análogo para a função , temos:
Como também se trata de uma função exponencial, a curva é uma hipérbole. Plotando os pontos no gráfico, temos:
Finalmente, colocando ambas as curvas em um mesmo gráfico, temos:
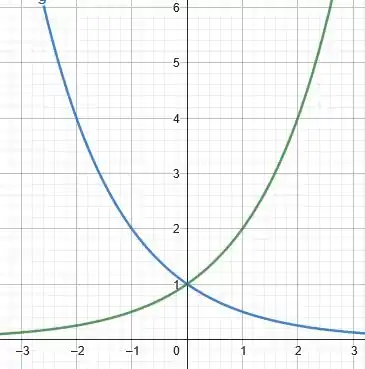
Olha que legal! Se olharmos direitinho, vemos que a função é a reflexão de em relação ao eixo . Isso ocorre porque, na prática, é como se tivéssemos:
Muito bom gente! Matamos mais uma questãozinha, até a próxima 😊
Resposta
