UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 4
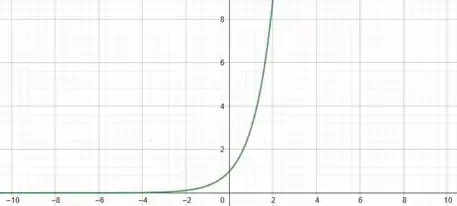
Faça o gráfico das funções abaixo montando uma tabela de valores. Se necessário, use uma calculadora.
Passo 1
Fala aí galerinha, tudo na paz com vocês?
Nessa questão precisamos montar o gráfico de duas funções:
Para fazer isso, iremos montar uma tabela de valores de e de seus respectivos resultados em e em . Podemos inclusive usar calculadora pra encontrar esses resultados, beleza?
Então, vamo nessa!
Passo 2
Bom, começando pela função precisamos selecionar alguns valores de para montar uma tabela e a partir daí desenhar o gráfico.
Antes de tudo é importante percebermos que tratam-se de duas funções exponenciais, ou seja, o gráfico é uma hipérbole.
Sabendo disso, vamos escolher valores de que nos ajudem a desenhar essa hipérbole.
Temos valores em volta do eixo , como também valores mais afastados pra determinar a tendência da função tender a zero ou a infinito.
Assim, podemos montar a tabela, usando a calculadora pra facilitar a cálculo dos resultados:
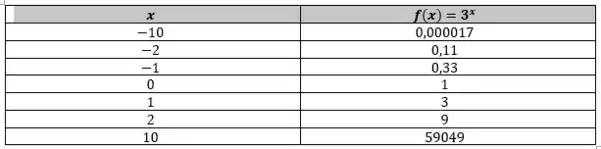
Passo 3
Massa! Agora que já montamos a nossa tabela, vemos que quando a nossa função também cresce bastante, tendendo a infinito. Já quando , temos que . Sendo assim, vamos plotar os valores encontrados em um gráfico e ligar os pontos seguindo o formato de uma hipérbole.
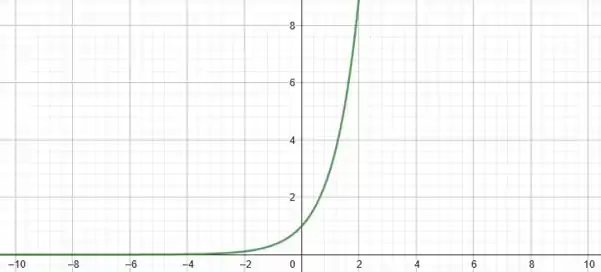
Muito bom! Vamos agora para o item .
Passo 4
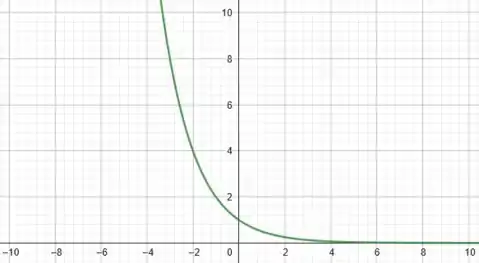
Vamos seguir o mesmo raciocínio para a função:
Assim, vamos montar a nossa tabelinha com o auxílio da calculadora:
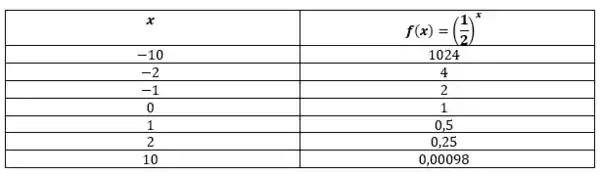
Muito bom! Assim, vemos que quando tende a infinito, nossa função tende a zero. Já quando , a nossa função cresce indefinidamente.
Portanto, podemos plotar esses pontos em um gráfico e traçar a curva da hipérbole. Temos:
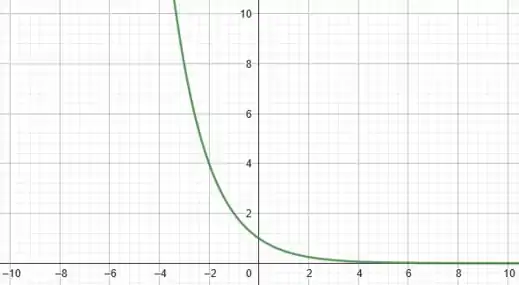
Excelente pessoal! Espero que vocês tenham entendido bem a solução 😊
Resposta
