UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 7ab
Faça o gráfico das funções abaixo, partindo de gráficos conhecidos.
Passo 1
Eaí gente, tudo tranquilo por aí?
Nessa questão precisamos desenhar o gráfico de duas funções exponenciais dadas, mas o enunciado nos pede para partir de gráficos conhecidos.
A ideia aqui é considerarmos o gráfico mais básico para cada função exponencial, e analisar o que a nossa função está fazendo com esse gráfico.
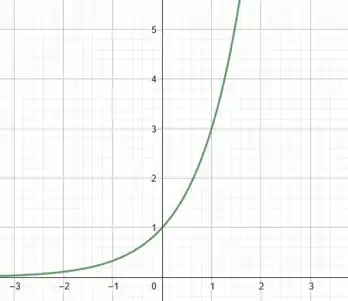
No item por exemplo, temos a função . A nossa função básica seria .
Daí, conhecendo o gráfico de , que é apenas uma hipérbole bonitinha, vamos analisar a influência do sinal negativo que aparece na .
Sacaram?
Então beleza, vamo lá!
Passo 2
Começando pelo item , temos a nossa função básica dada por:
O seu gráfico é uma hipérbole que vai para infinito quando , e que vai para zero quando . Ou seja, o gráfico é assim:
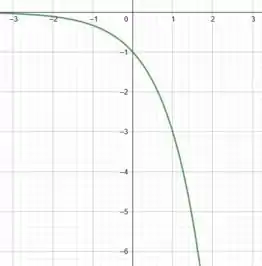
Agora, se multiplicarmos essa função por , o que será que acontece com esse gráfico?
Então gente, quando multiplicamos por , pra cada ponto que tínhamos agora vamos ter . É como se estivéssemos trocando os valores positivos da função por seus simétricos negativos.
Na prática, quando multiplicamos a função por estamos refletindo ela em relação ao eixo .
Assim, vamos ter o seguinte gráfico para :
Excelente!
Passo 3
Indo agora para o item , temos a função:
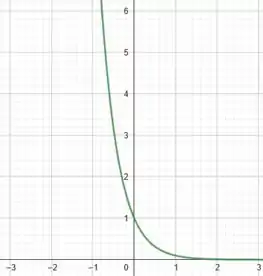
Assim, a nossa função base será:
E, a grande diferença entre e é que em o aparece multiplicado por . É como se na prática, tivéssemos:
Bom, o gráfico da função mais básica, , é também uma simples hipérbole que vai pra infinito quando . Assim, temos:
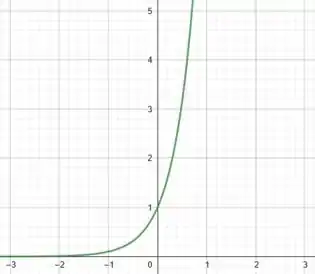
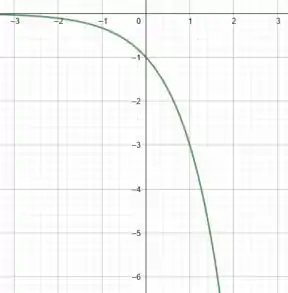
Massa! Vamos pensar a influência então de multiplicarmos o por .
É como se estivéssemos invertendo os resultados de entre os valores de negativo e seus simétricos positivos. Por exemplo, se tomarmos , temos que:
Encontraremos o mesmo resultado se tomarmos o simétrico de , ou seja, em . Olha:
Sendo assim, na prática estamos refletindo o gráfico de com relação ao eixo . Daí, temos o seguinte gráfico para :
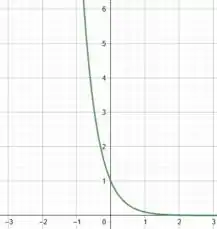
É isso aí galera! Até a próxima 😊
Resposta
