UFF, Sem Campus, Cálculo IIA, Avaliações a Distância (AD) - AD1 - 2023.1, Questão 2a
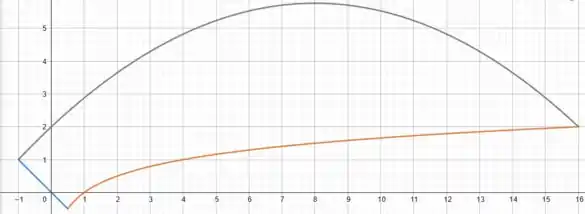
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Esboce a região .
Passo 1
Fala aí pessoal, tudo certinho?
Nessa questão recebemos funções que delimitam uma região .
Além disso, o enunciado também nos informou os pontos em que ocorrem intersecções dessa curva na região , ou seja, os vértices de : .
O nosso objetivo aqui é esboçar a região .
Pra fazer isso iremos analisar cada um dos pontos de intersecção, pra saber quais curvas se encontram em cada um deles. Assim, saberemos quais curvas delimitam em um certo intervalo em .
Após isso, podemos esboçar essas curvas em cada um desses trechos e finalmente esboçar a região. Beleza? Vamo nessa!
Passo 2
Bom, vamos começar analisando os pontos de intersecção.
Em , quais das curvas se intersectam?
Pra descobrir isso, podemos calcular o valor de cada uma das funções para . Vamos ter:
Olha aí, a função sequer é definida em , pois o seu domínio é todo positivo.
Logo, as curvas que se encontram nesses pontos são:
Assim, significa que no intervalo de até , as curvas que delimitam a nossa região são essas duas acima.
Vamos verificar agora em quais curvas estão se intersectando:
Agora, em as curvas que estão se intersectando são as duas últimas. Como esse é um vértice intermediário, significa que nesse ponto está havendo uma troca entre as duas curvas que se intersectam. Como assim?
Vimos que de até as curva que delimitavam era o polinômio do grau e a reta . Agora, em teve uma intersecção entre a reta e a curva logarítmica, isso significa que agora a curva logarítmica passará a definir a região junto com a curva do grau.
Isso ocorrerá até o último vértice, que ocorre em . Nesse ponto deverá ocorrer outra intersecção entre essas mesmas curvas a fim de fechar a região . Olha só, quando :
Viramm?
Assim, concluímos que:
No intervalo , a região é delimitada pelas curvas:
No intervalo , a região é delimitada pelas curvas:
Muito bom pessoal!
Passo 3
Agora que já sabemos quais curvas delimitam a região em cada um dos intervalos, vamos buscar esboçá-las nesse trecho.
Começando pela curva:
Trata-se de uma parábola, com concavidade virada para baixo. Ela estará definindo a região durante todo o intervalo:
E, como vimos no passo anterior, durante esse intervalo ela é sempre positiva. Então, vamos esboçá-la:
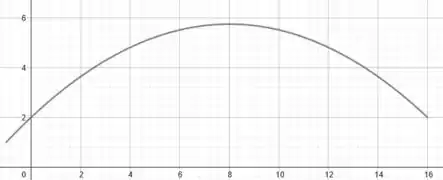
Massa!
Sabemos também que, no intervalo:
a reta delimita inferiormente a região .
A sua curva é uma reta, que passa pelo ponto , é decrescente, e tem ângulo de com o eixo e . Assim:
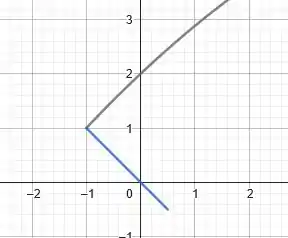
Onde a reta azul é a nossa reta e a curva cinza é a parábola que havíamos desenhado anteriormente.
Por fim, no intervalo:
Temos a curva:
delimitando inferiormente a nossa região . Trata-se da curva logarítmica mais clássica mesmo. Vamos desenhá-la:
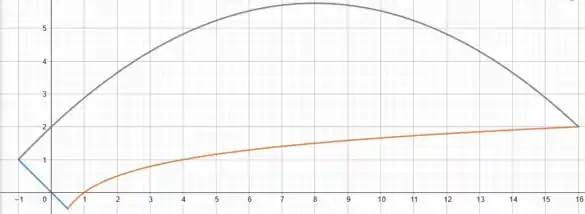
Prontinho galera! Essa é a nossa querida região .
Eaí, conseguiram entender tudinho? Responde Aí!
Resposta
