UFSC – Cálculo C – P1 – Questão 4-Parte I
Considere a região de intersecção de com . Esboce a região
Passo 1
E aí pessoal, tudo bem? O problema nos deu essas duas equações aqui
E pediu para não só calcular o volume entre as duas curvas, como também esboçar a região de intersecção.
A resolução ficaria pouco longa, então resolvi dividir em duas partes: nessa primeira parte vamos esboçar essa região, para entender como essas curvas estão dispostas no espaço. Já na parte (ii) vamos calcular o volume!
Mas como fazer isso?
Vamos analisar uma equação e cada vez! Começando pela de cima
No espaço tridimensional, quando temos todos os termos ao quadrado, temos uma esfera! E nesse caso repare que queremos a região interna, pois !
Sendo assim temos uma esfera de raio
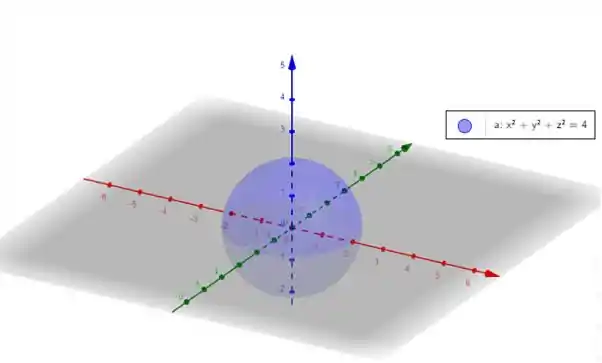
E a outra equação?
Precisamos organizar um pouco os termos para ver qual equação temos
Note que a variável é livre e as outras têm potência , então temos um cilindro (deslocado nesse caso em ) e de raio
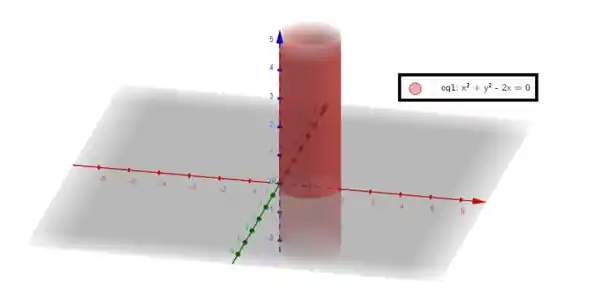
A ideia para ver qual é a região de interseção é juntar esses dois esboços em um só! Note que temos limitação no por causa da esfera! Se não tivéssemos essa limitação, nossa região seria infinita, porque o cilindro é infinito na direção de
Bora juntar esses dois esboços?
Passo 2
Temos que em a limitação é feita através da esfera
Então temos que
Tranquilo até aqui?
Agora vamos pensar na intersecção das outras curvas. Mas para ver isso, vamos fazer
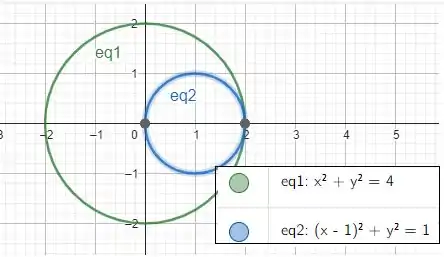
Queremos a região entre essas duas curvas!
Em coordenadas cilíndricas
Então nossa região fica
E com a ajuda de um software gráfico temos a intersecção:
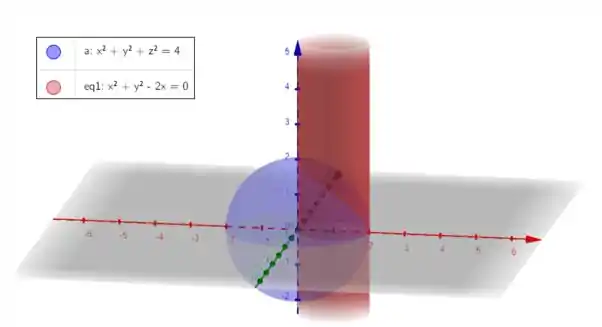
E é isso! Agora na parte II vamos calcular o volume dessa intersecção!
Vamos para a próxima parte?
Resposta
Ei, a resposta está no passo a passo :)