UFSC – Cálculo C – P1 – Questão 2(ADAPTADO) – Parte I
Considere a área da região de intersecção às curvas e .
Parte I) Esboce a região
Passo 1
E aí pessoal, tudo bem? O problema nos deu essas duas curvas aqui em coordenadas polares
E pediu não só para esboçar a região de intersecção, mas também calcular a área da região esboçada. Como a resolução ficaria pouco longa vamos fazer assim: dividir em duas partes. Nessa primeira parte vamos fazer apenas o esboço. Na parte (ii) será calculada a área dessa região. Ok?
#partiu fazer o esboço!
Mas como fazer isso?
Quando temos curvas em polares e queremos achar a região, precisamos saber qual é essa intersecção, não é verdade?
Então vamos começar juntando as duas equações
Mas , daí
Mas
Assim temos que
E isso acontece quando . O ponto onde as curvas se encontram é esse! Mas tem mais um né! Vamos olhar para as curvas originais
Quando ou ambas resultam em , então temos nosso limite de integração!
E isso vai ser encontrado naturalmente no gráfico!
A ideia daqui para frente é esboçar cada uma e depois agrupar os resultados!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Começando com . Sabemos que em coordenadas polares isso representa um círculo deslocado em , com raio
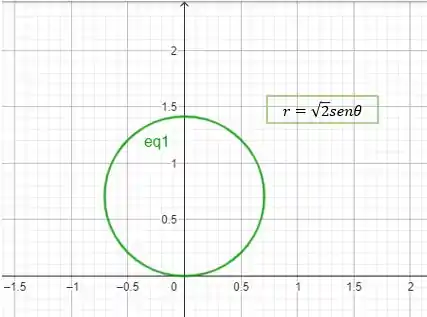
Beleza?
Passo 3
Agora vamos para o esboço da outra equação
Essa é uma equação de uma Lemniscata, e como ela vai com o seno e seu coeficiente é positivo, é na diagonal que corta os quadrantes ímpares
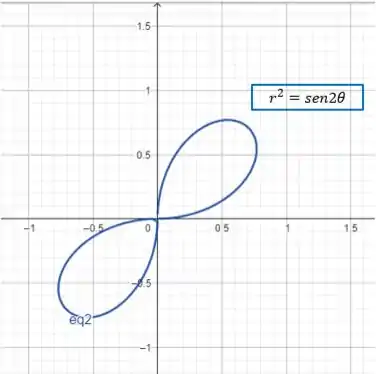
Tudo bem até aqui? Nosso próximo passo é juntar essas duas figuras!
Passo 4
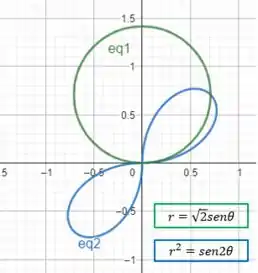
Sabemos que elas se cruzam em e em , então as duas juntas ficam assim:
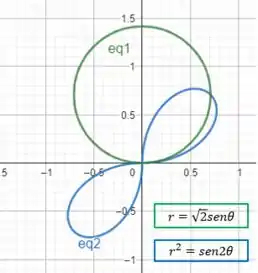
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta
