UFCG, Sem Campus, Cálculo Diferencial e Integral III, Listas - Profª Pamella Queiroz - Lista 1 - 2022.1, Questão 1.2ef
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Passo 1
Oiie, tudo bem?
O enunciado nos dá duas funções, sendo elas
precisamos construir curvas de nível para cada função de forma que possamos visualizar o seu gráfico! Para isso, precisamos dar valores , em que é uma constante real! E, assim vamos montando a superfície desejada! Vamos lá!
Passo 2
Temos primeiro que
Vamos começar com , temos que
ou seja, nossas curvas de nível são as seguintes retas
Que podem ser representadas como
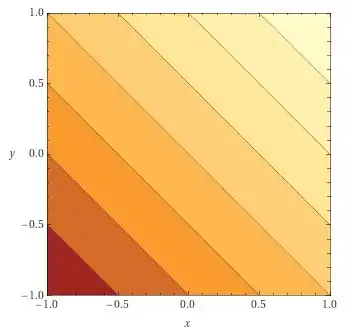
e, o seu gráfico é tal que
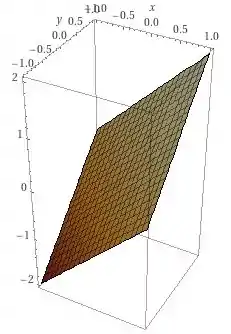
Essa é a primeira alternativa! Bora para a próxima!
Passo 3
Temos a seguinte função
Se igualarmos a uma constante qualquer, temos que
aplicando a função inversa arcosseno em ambos os lados, temos que
nos dando o seguinte conjunto de retas
Mas neste caso apenas varia de . Obtemos então a seguinte representação
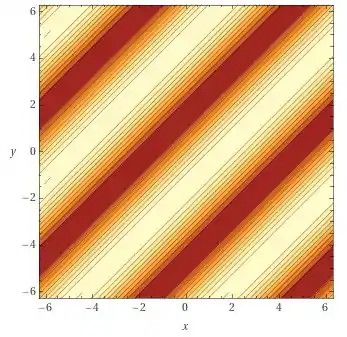
e, o gráfico é tal que
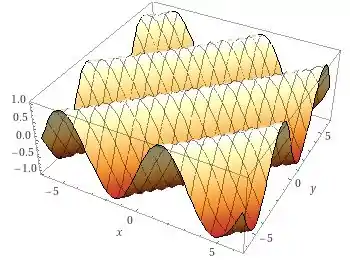
Maravilha! A questão foi isso! Te vejo na próxima! Tchau Tchau!