UFPE, Sem Campus, Cálculo 3, Listas de Exercícios de Cálculo 3 - Profº Cilon Perusato - Lista 1, Questão 5
Uma curva polar consiste em todos os pontos que têm pelo menos uma representação cujas coordenadas satisfazem a equação. Por exemplo, a curva representada pela equação é um círculo de raio e centro na origem. A curva é uma reta que passa na origem com inclinação radiano. Desta forma, esboce a curva polar . Calcule a inclinação de sua reta tangente quando . Encontre todos os pontos onde a reta tangente é horizontal e vertical.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma curva polar e pediu pra gente esboçar essa curva, calcular a inclinação de sua reta tangente quando e verificar todos os pontos onde a reta essa reta tangente é horizontal e vertical.
Para esboçar a curva polar, vamos primeiro esboçar o gráfico de em coordenadas cartesianas, em seguida, vamos comparar os valores de nos intervalos crescentes e decrescentes de . Para calcular a inclinação da reta tangente, vamos usar o método para encontrar inclinações de curvas parametrizadas, que nos fornece a equação:
Em seguida, aplicamos para obter a inclinação nesse ponto. Por fim, vamos localizar as tangentes horizontais achando os pontos onde (desde que ) e localizamos as tangentes verticais nos pontos onde (desde que ).
Vamos lá!
Passo 2
Vamos começar o gráfico da função em coordenadas cartesianas, pelo deslocamento da curva seno em uma unidade para cima:
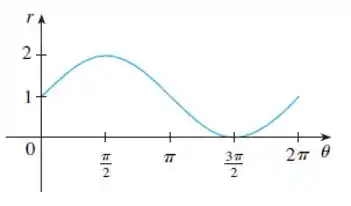
Isso nos permite ler de uma vez os valores de que correspondem aos valores crescentes de . Por exemplo, vemos que quando aumenta de até , (a distância a partir da origem) aumenta de até . Assim, esboçamos a parte correspondente da curva por na figura:
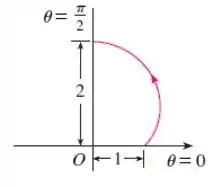
Quando aumenta de até , o gráfico cartesiano mostra que diminui de até e, dessa forma, esboçamos a outra parte da curva:
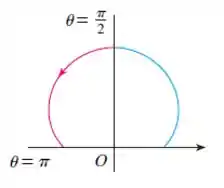
Quando aumenta de até , diminui de para . Assim:
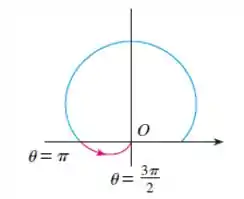
Finalmente, quando aumenta de até , aumenta de para :
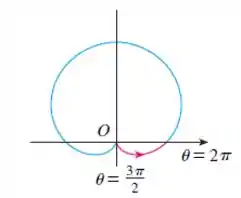
Se a gente deixasse aumentar além de ou diminuir além de , simplesmente iríamos traçar novamente essa trajetória. Então, juntando todas as partes, temos o esboço completo dessa curva que é chamada de cardioide, porque tem o formato parecido com o de um coração:
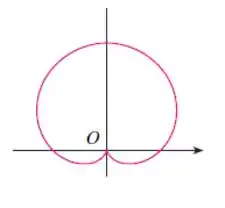
Passo 3
Agora vamos calcular a inclinação da reta tangente de usando a expressão:
Derivando em em relação a , temos . Então, substituindo e na expressão, temos:
Colocando em evidência no numerador e usando no denominador, encontramos:
Essa é a equação da nossa reta tangente. Em , temos a inclinação:
Como e , temos:
Simplificando:
Passo 4
Para localizar as retas tangentes horizontais vamos fazer . Lembrando que . Como calculamos no início do passo , temos:
Isso acontece quando .
Para localizar as retas tangentes verticais vamos fazer . Lembrando que e nós também já calculamos lá em cima, temos:
Isso acontece quando .
Portanto, temos tangentes horizontais nos pontos , , e tangentes verticais em e . Quando , e são e, dessa forma, temos que ser cuidadosos. Calculando os limites laterais nesse ponto, vemos que a reta tenta a e a , portanto, existe uma reta tangente vertical no polo. Podemos ver isso na figura:
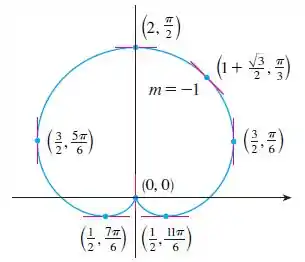
Prontinho, galera! Até a próxima! 😉
Resposta
, ,
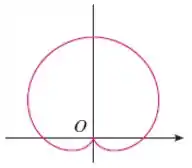
e