UFCG, Sem Campus, Cálculo Diferencial e Integral III, Listas - Profª Pamella Queiroz - Lista 1 - 2022.1, Questão 1.6cd
Esboce o gráfico da função .
Passo 1
Eaew, tudo certinho contigo?
Temos que esboçar os gráficos das seguintes funções
esboçar gráficos de funções de várias variáveis não tem uma receitinha de bolo como no caso de uma função de variável! Então, é bastante uma análise de caso a caso! Vem comigo!
Passo 2
A primeira função é tal que
Por simplicidade, vamos analisar a função em cada plano. Primeiro, quando , temos a seguinte reta no plano
quando temos que , temos a seguinte reta no plano
Como informação adicional, as curvas de nível são obtidas fazendo , em que obtemos
nos dando as retas
Com essas informações podemos obter o gráfico como
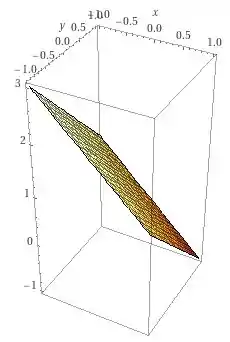
Essa primeira alternativa é só isso! Vamos para a próxima!
Passo 3
Agora, temos a seguinte função
note que a função não depende de , portanto, para todo valor no eixo , teremos a função senoidal
Então, você pode imaginar um gráfico de um seno, que é arrastado por todo o eixo do gráfico da superfície, temos o seguinte
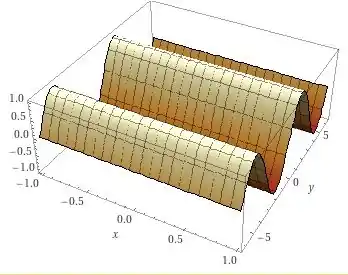
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!