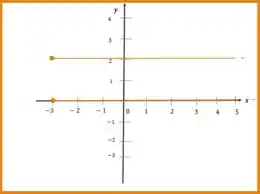
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Passo 1
E aí pessoal, tudo bem? O problema nos esses dois conjuntos
e pediu para representarmos graficamente o produto cartesiano no plano cartesiano. Mas, como fazer isso?

O produto cartesiano é um conjunto formado pelos pares ordenados envolvendo os elementos dos dois conjuntos dados
 Ué, como assim?
Ué, como assim?
Se tivermos dois conjuntos com elementos, vamos resgatar do primeiro elemento a abscissa e do segundo conjunto a ordenada do ponto
Fazendo o produto cartesiano temos que as abscissas dos pontos vêm de e a ordenada de
Então vamos ter quatro pontos! Se a ordem for trocada, vamos ter outros pontos, aqui precisamos ter atenção!
Beleza?

E se algum desses conjuntos for um intervalo? Então não vamos ter pontos e sim segmentos de retas! Isso mesmo! Aqui você precisa ter atenção se o intervalo é aberto ou fechado, isso vai ser importante no início e no fim do seu segmento (bolinha aberta ou fechada)
 Mas relaxa, vou fazer passo a passo com você!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossos conjuntos são de elementos, então teremos pontos
Queremos saber : lembrando que os elementos do primeiro formam as abscissas e do segundo as ordenadas. Como temos intervalo em e elementos em , vamos ter retas no espaço! Pois temos infinitos pontos em e apenas uma ordenada em ! Vamos colocar no plano cartesiano primeiro e ver no que dá
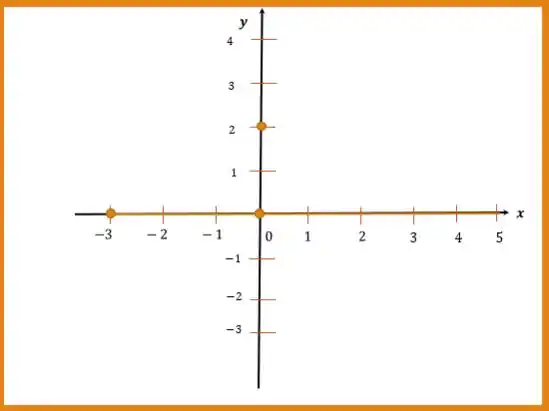
Percebe que não temos um limite superior em ? isso significa que teremos retas horizontais infinitas. Teremos duas retas horizontais, com e com , saindo do sem limite superior
 Tranquilo até aqui?
Tranquilo até aqui?
Agora precisamos representar em um gráfico esses segmentos!
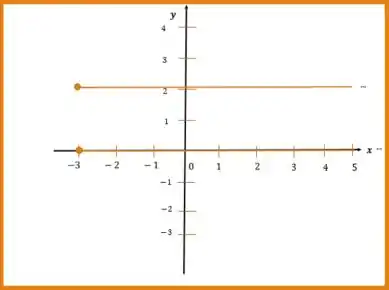
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta