UFSC – Pré Cálculo – Lista 2 – Questão 13d
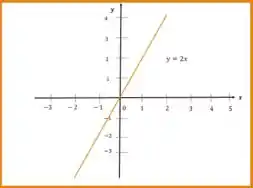
Representar graficamente, no plano cartesiano, os conjuntos abaixo
Passo 1
E aí pessoal, tudo bem? O problema deu esse conjunto
E pediu para representar graficamente. Mas como?
Precisamos olhar em que mundo estamos, e isso diz logo no começo da sentença, antes daquela barra , no nosso caso
Sabemos que estamos em um espaço bidimensional! Então precisamos representar a sentença que vem depois da barra no plano:
Em isso significa uma reta! Temos que para cada valor de , temos que a ordenada vale o dobro!
A ideia para resolver essa questão é representar essa reta no plano cartesiano! E quando você tiver outra sentença, a ideia é estabelecer uma relação entre as variáveis e , desenhar pontos, e fazer uma correspondência com os gráficos que conhecemos (potência , linear, potência parábola e assim em diante)
Beleza?
Mas fica tranquilo, vou fazer passo a passo com você!
Passo 2
Nosso conjunto , vamos ver quais os valores de alguns pontos
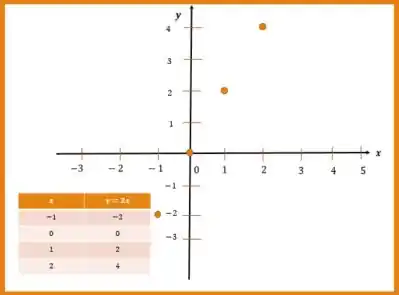
Mas temos um conjunto contínuo tanto em quanto em , então podemos adicionar inúmeros pontos entre esses que estão no plano, mas sempre seguindo a mesma regra
Isso fará com que tenhamos uma reta! Vamos ver como fica em um gráfico?
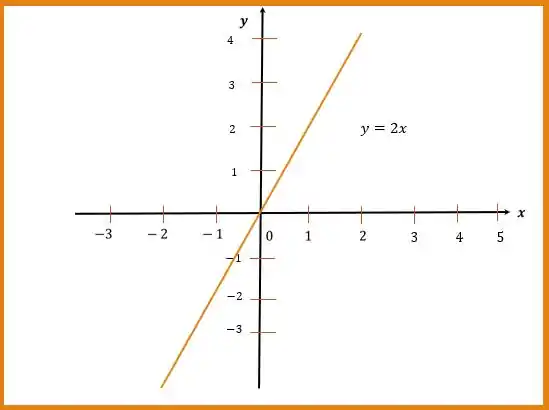
Tranquilo?
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta
