UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 7cd
Faça o gráfico das funções abaixo, partindo de gráficos conhecidos.
Passo 1
Fala aí gente bonita, tudo bom com vocês?
Nessa questão precisamos desenhar o gráfico de duas funções exponenciais dadas, mas o enunciado nos pede para partir de gráficos conhecidos.
A ideia aqui é considerarmos o gráfico mais básico para cada função exponencial, e analisar o que a nossa função está fazendo com esse gráfico.
No item por exemplo, temos a função:
A nossa função básica, cujo gráfico é conhecido, deverá ser . Assim, precisamos analisar qual o efeito de subtrair unidades no gráfico de . Pegaram a ideia?
Então vem comigo!
Passo 2
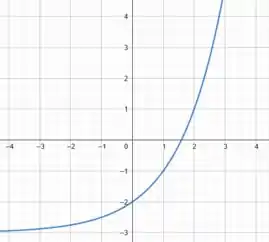
Começando pelo item , precisamos determinar o gráfico de
O gráfico conhecido, como comentamos no passo anterior, é o de . Trata-se de uma hipérbole gente, e pra desenhá-la basta lembrarmos que quando a função também vai para o infinito. Assim, temos o seguinte gráfico:
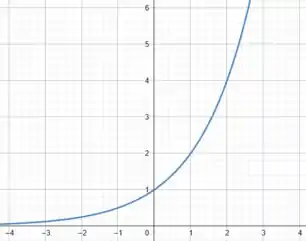
Mas, o que acontece com essa curva se subtrairmos unidades?
Então, é o que chamamos de transladar o gráfico para cima ou para baixo. Como estamos subtraindo, toda a curva deve ser deslocada unidades para baixo. Isso é o mesmo de subir o eixo três unidades para cima. Ficamos com:
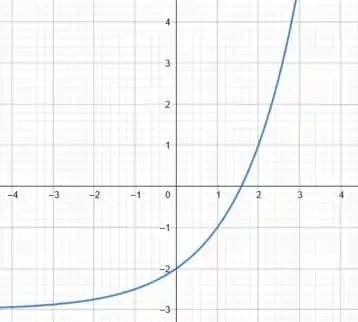
Massa! A primeira parte já foi!
Passo 3
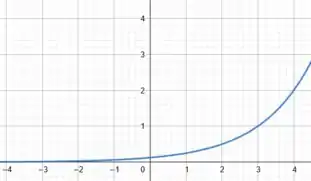
Agora vamos para o item . Aqui precisamos desenhar o gráfico da função:
Aqui a situação é um pouco diferente, porque subtraímos três unidades no expoente, e não na função como um todo. Na prática, podemos chamar:
Assim, nossa é equivalente a:
Ou seja, a curva tem a mesma característica do gráfico de que virmos anteriormente. A diferença é que , ou seja, é como se estivéssemos transladando toda a curva para a direita. Assim, temos o seguinte gráfico:
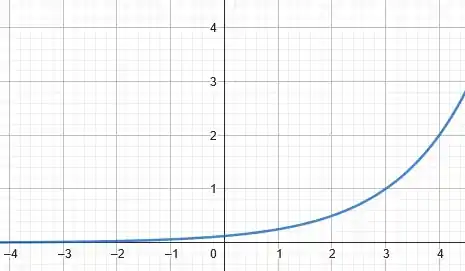
Prontinho!! Entenderam bem? Responde Aí!
Resposta
