UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 6
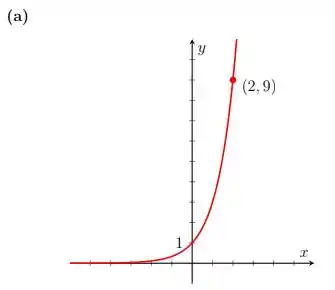
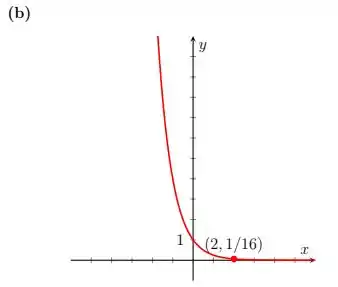
Encontre a função exponencial cujo gráfico está representado.
Passo 1
Fala aí galera, tudo na paz por aí?
Nessa questão recebemos dois gráficos de funções exponenciais e precisamos determinar a lei da função a partir desses gráficos.
Em cada um desses gráficos temos a informação sobre um ponto pertencente a curva da função, e é justamente isso que iremos utilizar.
Como falado no enunciado sabemos que a função é do tipo:
Então, se conhecemos um ponto sabemos que:
Daí, podemos escrever também na forma exponencial, e aí é só igualar as bases.
Vem comigo que vai ficar bem claro 😊
Passo 2
Então, começando pelo item , temos:
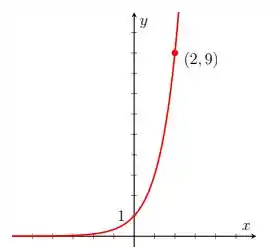
Daí, usando o ponto dado, temos que:
Mas, podemos reescrever esse como:
Daí:
Ou sejaaa, é só igualarmos as bases:
Logo, a nossa função é dada por:
Passo 3
Indo agora para o item , temos:
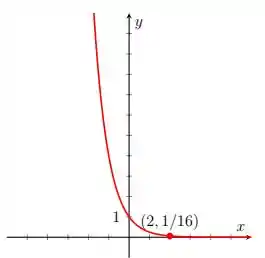
Usando o ponto dado, temos:
Mas, podemos escrever como:
Daí, temos:
Igualando as bases, vamos ter:
Assim, a nossa função vale:
Prontinho! Com isso matamos mais uma questãozita!
Obrigado pela atenção gente 😊