UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 26
Faça o gráfico das funções abaixo montando uma tabela de valores. Se necessário, use uma calculadora.
.
.
Passo 1
E aí gente, como vocês estão?
Nessa questão recebemos duas funções logarítmicas e precisamos desenhar os seus gráficos. Para isso, devemos montar uma tabela de valores e em função de .
Relembrando também o formato do gráfico da função logarítmica (quando a base é maior do que ):
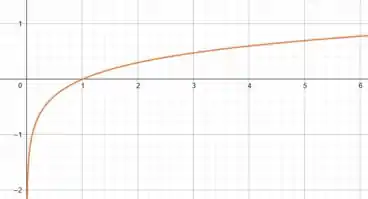
Massa! Com as informações da tabela de valores que vamos fazer, e conhecendo o formato da curva da função logarítmica podemos desenhar essas funções. Vem comigo 😊
Passo 2
Bom, começando pelo item , temos a função:
Lembrando que o domínio da função logarítmica é nos reais não-negativos, vamos montar a seguinte tabela:
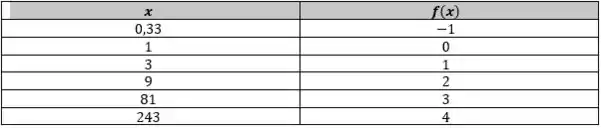
De posse dessa tabela já podemos esboçar a nossa curva de :
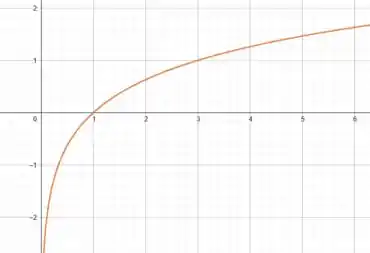
Muito bom!
Passo 3
Já agora no item , temos a função:
Novamente, o nosso domínio é composto pelos reais não-negativos. A grande diferença aqui é que, como a nossa base é , a função é decrescente. Então, a curva ainda tem um formato parecido, mas agora deve tender para o infinito quando . E, a medida que cresce, se torna mais negativa.
Vamos fazer nossa tabelinha de valores pra deixar isso mais claro:
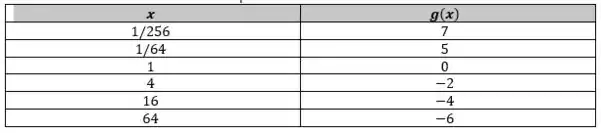
Viu? O crescimento dessa função é contrário da do item . Bom, reunindo todas essas informações, podemos esboçar a sua curva:
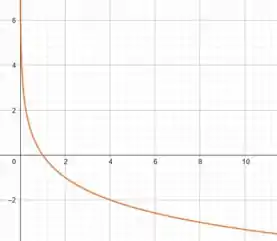
Prontinho! Conseguiram entender bem a solução? Responde Aí!
Resposta
Resposta no texto.