UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 11
Utilize o gráfico da função para fazer os gráficos das funções abaixo.
.
.
.
.
Passo 1
Fala aí pessoal, tudo certinho?
Então, nessa questão precisamos desenhar o gráfico de quatro funções:
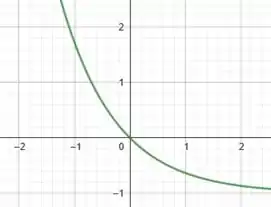
Mas, para fazer isso podemos usar de antemão o conhecimento do gráfico da função , que é dado por:
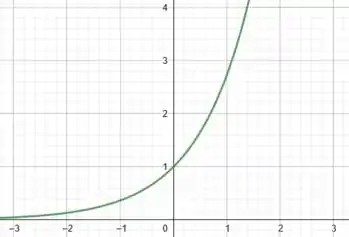
Pois bem pessoal, a grande ideia aqui nessa questão é entendermos como as operações matemáticas vão influenciar o gráfico da função. Então, bora dar uma revisada nos pontos mais importantes:
Se transladamos o gráfico de uma função em unidades pra cima, é porque matematicamente fizemos:
- Se transladamos o gráfico de uma função em unidades pra baixo, é porque matematicamente fizemos:
- Se transladamos o gráfico de uma função em unidades pra esquerda, é porque matematicamente fizemos:
- Se transladamos o gráfico de uma função em unidades pra direita, é porque matematicamente fizemos:
- Se refletimos o gráfico de uma função em relação ao eixo , é porque matematicamente fizemos:
- Se refletimos o gráfico de uma função em relação ao eixo , é porque matematicamente fizemos:
Massa! Então vamo aplicar essas ideias em cada um dos gráficos!
Passo 2
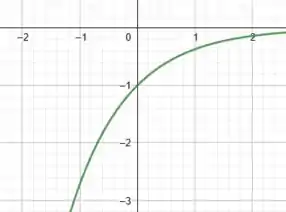
Começando pelo item , temos a função:
Então, tudo que fizemos em relação à nossa função base foi multiplicar por . Mas, como vimos no passo anterior, multiplicar por é equivalente a refletir a função com relação ao eixo . Assim, teremos para o gráfico de :
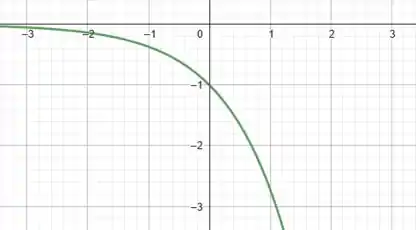
Muito bom!
Passo 3
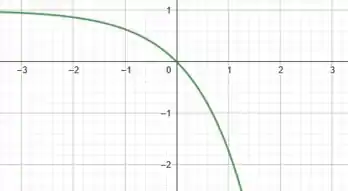
Indo agora para o item , precisamos desenhar o gráfico da função:
Comparando com a nossa função base ), vemos que multiplicamos ela por e depois somamos uma unidade à função como um todo.
Como comentamos no passo anterior, multiplicar por é o mesmo que refletir a curva em relação ao eixo . Assim, temos o gráfico:
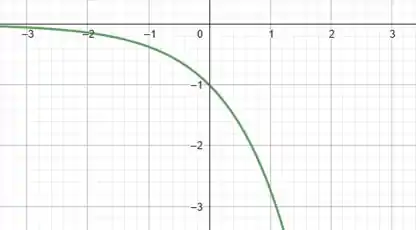
Porém, também somamos uma unidade à função como um todo. Quando fazemos isso estamos transladando toda a curva para cima em uma unidade. Assim, temos o gráfico:
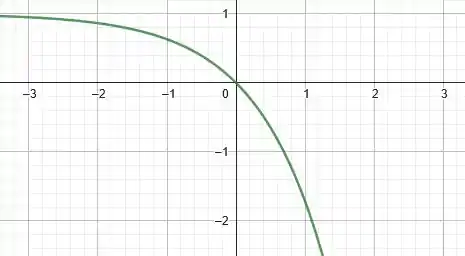
Tudo tranquilo até aqui? Vamo pro próximo!
Passo 4
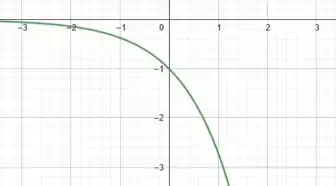
No item temos a função:
Novamente, comparando com a nossa função base ), vemos que multiplicamos o por e também subtraímos uma unidade à função como um todo.
Bom, multiplicar o termo por é equivalente a refletir a função em relação ao eixo . Daí, temos:
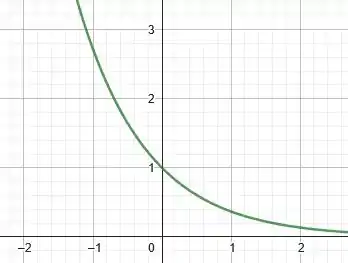
Já quando subtraímos uma unidade à função como um todo, estamos transladando a função verticalmente uma unidade para baixo. Assim:
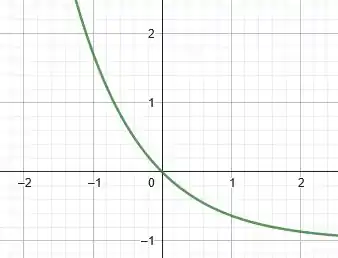
Excelente!
Passo 5
Por fim, no item temos a função:
O que fizemos aqui foi multiplicar tanto o termo em como a função inteira por . Ou seja, temos uma dupla reflexão: refletimos a curva de tanto em relação ao eixo como em relação ao eixo .
Fazendo isso temos:
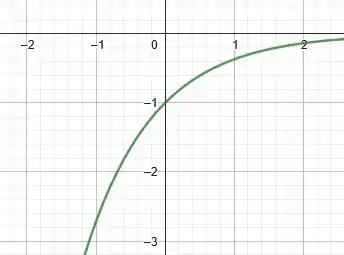
Muito bom galera!
Com isso finalizamos a questão, muito obrigado pela atenção 😊
Resposta
