UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 14
A função é definida como
Calcule e
Qual é o domínio desta função?
Verifique que esta função é ímpar.
Faça o gráfico. Sugestão. Faça o gráfico de e e utilize a subtração de gráficos.
Passo 1
Ooi pessoal, como vocês estão?
Nessa questão vamos trabalhar um pouco a definição da função .
Como o enunciado nos falou, ela é definida através da função exponencial pela relação:
Precisaremos calcular o para , basicamente iremos substituir por esses valores dentro da função
Também iremos determinar o domínio da função Aqui a ideia é verificar se há alguma restrição nos reais segundo a lei de formação de
No item , provaremos que é uma função ímpar. Para isso, precisamos mostrar que:
E, por fim, iremos desenhar o gráfico da nossa querida função!
Então vamo nessa!
Passo 2
Começando pelo item , temos que calcular e .
Bora lá, basta substituir na expressão:
pelo valor que queremos.
Logo:
Para temos:
Usando a calculadora:
Por fim:
Pela calculadora:
Excelente!
Passo 3
No item precisamos verificar o domínio da função hiperbólica.
Aqui o nosso problema passa por verificar se tem alguma restrição na lei de formação do
Vamos detalhar um pouco mais a fórmula que nos foi dada:
A nossa função exponencial possui domínio em todos os reais. Assim, poderíamos ter algum problema no termo:
Pois, onde for teremos uma restrição. Mas, o massa é que a função nunca alcança o valor nulo, ela apenas tende a zero quando .
Logo, o domínio de é todo o conjunto dos números Reais.
Passo 4
No item devemos verificar se a função é par. Para fazer isso, precisamos verificar se a igualdade abaixo é verdadeira:
Vamos partir do lado direito e tentar chegar no lado esquerdo:
Mas, a expressão acima é justamente o Assim, concluímos que:
Portanto, de fato a função é ímpar.
Passo 5
Pra finalizar, no item precisamos desenhar o gráfico de
Nos é dada a sugestão de montar separadamente os gráficos de e , e depois subtrai-los.
Então, vamo seguir essa ideia!
Bora dar uma revisada no formato do gráfico de :
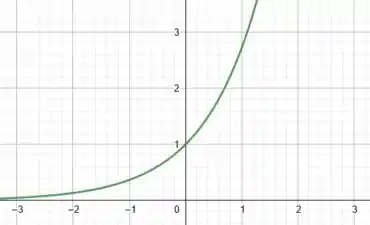
Para desenhar o gráfico de devemos entender que ao multiplicar por é como se tivéssemos encolhido a curva de por esse mesmo fator. Assim, temos o gráfico:
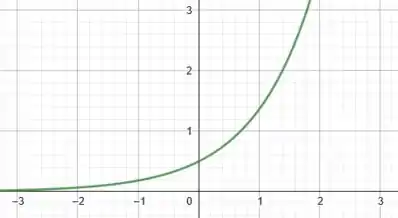
Já no gráfico de , primeiro multiplicamos o termo por . Isso é equivalente graficamente a refletir a curva de com relação ao eixo . Após essa reflexão o gráfico também foi encolhido pelo fator de . Assim, temos:
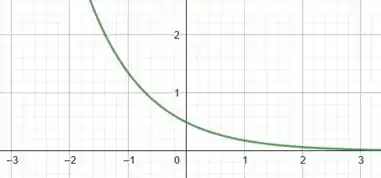
Muito bom! Agora é só fazermos a subtração dos dois gráficos. Vamos ficar com:
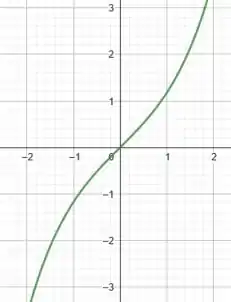
Ufaaa! Terminamos essa questão!
Espero que vocês tenham curtido a solução, até a próxima 😊
Resposta
Resposta no texto.