UFCG, Sem Campus, Cálculo Diferencial e Integral III, Listas - Profª Pamella Queiroz - Lista 1 - 2022.1, Questão 1.6ef
Esboce o gráfico da função .
Passo 1
Eaew, tudo certinho contigo?
Temos que esboçar os gráficos das seguintes funções
esboçar gráficos de funções de várias variáveis não tem uma receitinha de bolo como no caso de uma função de variável! Então, é bastante uma análise de caso a caso! Vem comigo!
Passo 2
A primeira função é tal que
Por simplicidade, vamos analisar a função em cada plano. Primeiro, quando , temos a seguinte função exponencial no plano
quando temos que , temos a seguinte reta no plano
Como informação adicional, as curvas de nível são obtidas fazendo , em que obtemos
aplicando o logaritmo neperiano em ambos os lados, temos que
Ou seja, o nosso gráfico tem níveis dados por circunferências de raio, . Sendo assim, podemos usar essa informação para desenhar um gráfico como
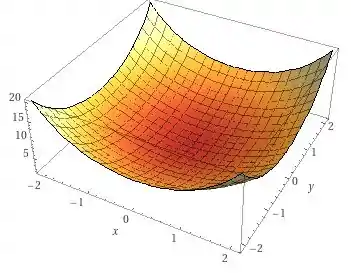
Essa primeira alternativa é só isso! Vamos para a próxima!
Passo 3
Agora, temos a seguinte função
quando fazemos , temos as seguintes parábolas no plano
e, quando , temos outras parábolas no plano
as curvas de nível são da forma
Que pode ser escrito como circunferências da forma
Então temos parábolas rotacionadas ao longo de circunferências de raio , sendo assim, o gráfico é
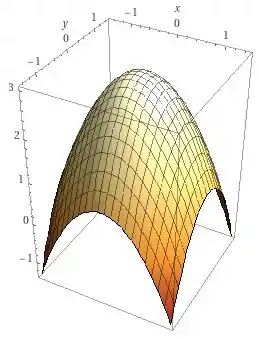
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!