UFPE, Sem Campus,Cálculo 1, Listas de Cálculo 1 - Lista de Derivadas 2022.2, Questão 8c
Considere a função definida por .
Esboce os gráficos de e .
Passo 1
Oiie, tudo certinho?
Temos uma função , com a definição
precisamos esboçar os gráficos de e . Nas alternativas anteriores nós usamos a definição de módulo para mostrar que
se e se
e, que
se e se
Então o esboço deste gráfico requer uma breve análise dos sinais nas funções acima! Saca só!
Passo 2
Note que para nossa função é uma parábola que passa pela origem! Da seguinte maneira
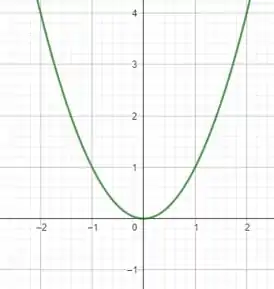
mas, note que devemos ter cuidado, pois para , temos que a nossa função toma a forma de uma parábola com concavidade para baixo (devido ao sinal negativo na frente) da seguinte maneira
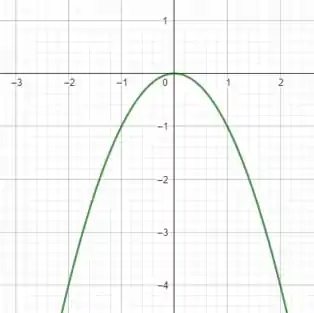
O nosso gráfico da função será a junção de ambas como
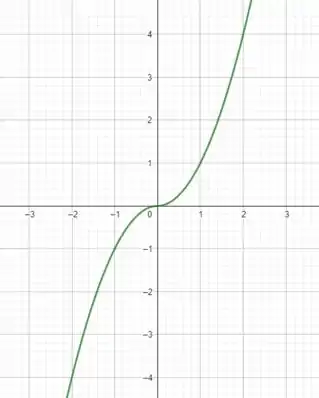
Vamos analisar o gráfico da derivada agora! Saca só!
Passo 3
A nossa derivada tem uma análise parecida, mas agora, temos a seguinte expressão
se e se
é uma reta de inclinação negativa que passa pela origem para , e uma reta de inclinação positiva que passa pela origem para . No entanto, como para a primeira reta temos que é sempre negativo, na verdade temos uma reta de inclinação positiva em ambos os casos, nos levando a simplesmente uma reta da forma
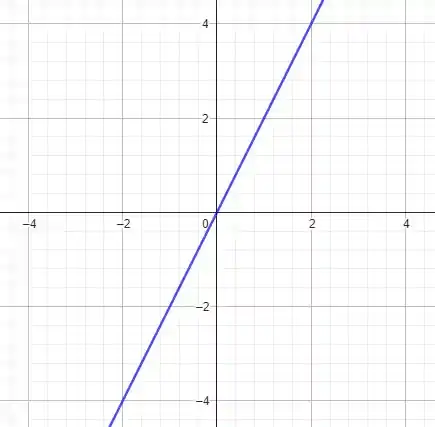
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!