UFPE, Sem Campus, Cálculo 3, Listas de Exercícios de Cálculo 3 - Profº Cilon Perusato - Lista 1, Questão 1
Esboce o gráfico da equação paramétrica dada por .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma equação paramétrica e pediu pra gente esboçar essa curva em um gráfico. Repare que e são funções de uma terceira variável, que é chamada parâmetro. Esse par de equações, descreve uma curva e cada valor de representa um ponto que podemos marcar em um plano coordenado.
Dessa forma, podemos montar uma tabelinha com os valores correspondentes de em cada ponto e unir esses pontos no plano cartesiano para produzir nossa curva.
Vamos lá!
Passo 2
Nossa equação paramétrica é dada por . Então, temos e . Vamos escolher alguns valores aleatórios de para ver como nossa curva se comporta:
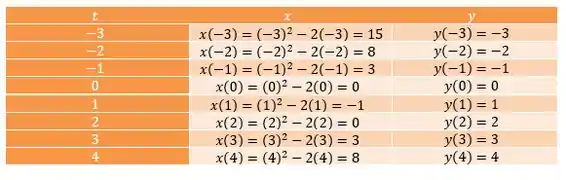
Beleza, agora vamos marcar os pontos no plano cartesiano:
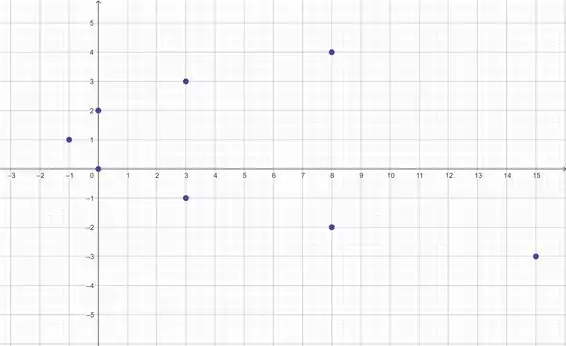
Unindo esses pontos, temos nossa curva:
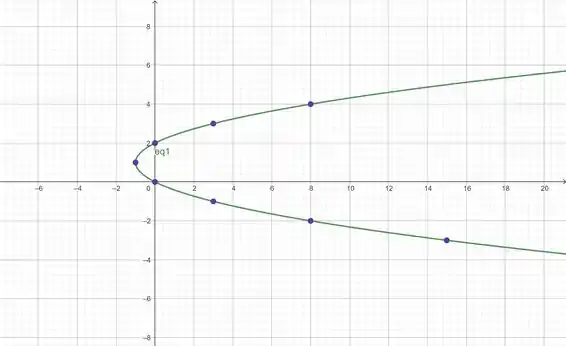
Prontinho, galera! Até a próxima! 😉