UERJ, Sem Campus, Cálculo I, Provas - Profº Alexandre - P1 2015.1, Questão 5
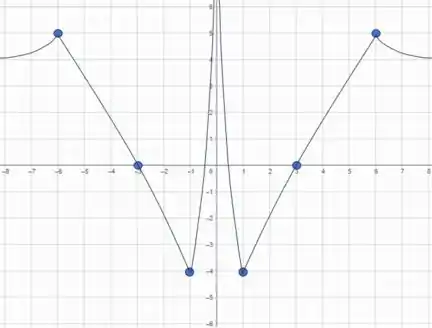
Esboce o gráfico de uma função que satisfaça todas as seguintes características:
é par
Passo 1
Eaee!!! Belezinha? Bom... queremos construir um gráfico com as seguintes características:
é par
Muita informação né??
Mas vamos com calma, analisando informação por informação, que aos poucos vamos construindo.
Ah, vamos lembrar de uma coisinha:
Uma função é considerada par quando .
Isso significa dizer que a função também deve respeitar os seguintes pontos:
Agora vamos lá!!
😉
Passo 2
Vamos começar primeiro marcando os pontos:
No gráfico, fica assim:
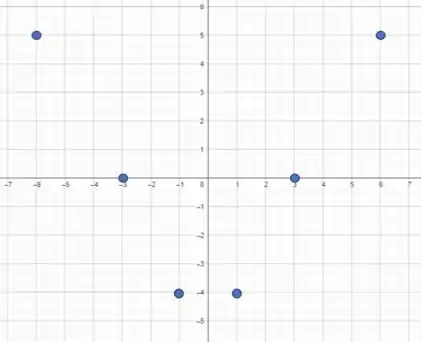
Passo 3
Agora, veja essa outra condição:
Ou seja, quando tende ao infinito negativo, se aproxima de 4, ou seja:
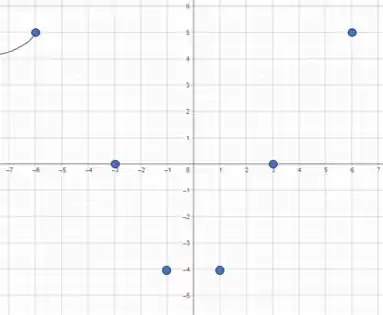
E como nossa função é par, então refletimos o que acabamos de fazer para o lado positivo:
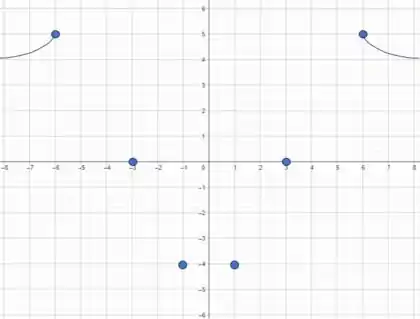
Passo 4
Continuando, veja essa outra condição:
Ou seja, quando tende a zero pelo lado negativo, tende ao infinito positivo, ou seja:
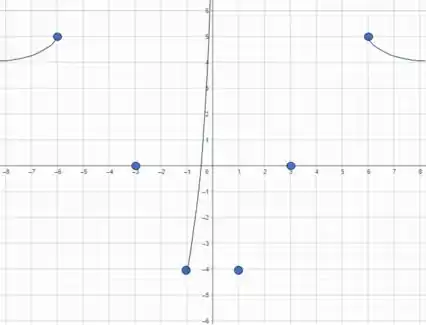
E como nossa função é par, então refletimos o que acabamos de fazer para o lado positivo:
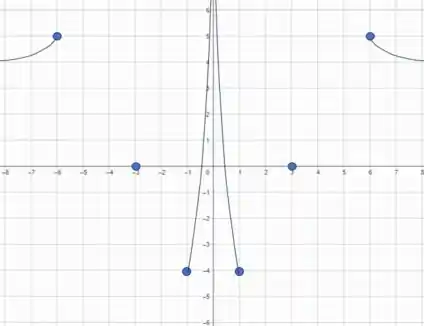
Passo 5
Por fim, cobrindo os pontos que ligamos no passo 2, temos a nossa função esboçada que respeita todas as condições que foram impostas:
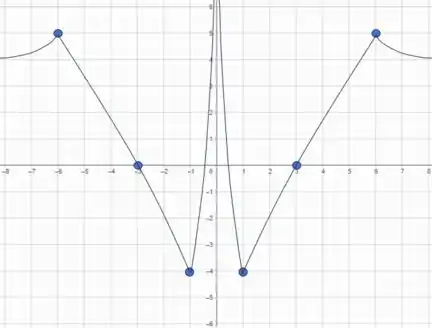
Entendeu direitinho? Responde aee ;)
Resposta
