Tarefa 2, Grau G2 - MAT 1163 Cálculo III – PUCRIO – Questão 2
Considere a curva parametrizada
(a) Esboce a curva e encontre seu comprimento.
(b) Encontre a posição do centroide da curva
Passo 1
a) Bom! Esboçar a curva é bem de boas!
Ela vai ter a seguinte cara...
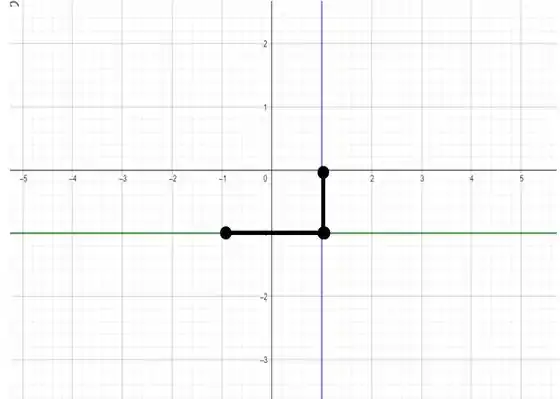
E o seu comprimento podemos obter visualmente... No caso, vai valer:
Passo 2
b) Agora é a hora de encontrar o centroide da curva!
Como podemos ver ela vai formar um triângulo retângulo...
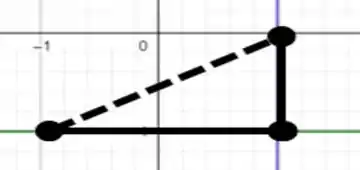
Pra achar o centroide, é só achar o centroide desse retângulo. No caso, as posições vão ser...
Resposta
a)
b)
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica