UFCG, Sem Campus, Cálculo Diferencial e Integral I, 3º Estágio - 2022.2, Questão 2
Faça o esboço do gráfico da função
destacando informações relacionadas a domínio, continuidade, derivabilidade, interseções com os eixos coordenados, assíntotas, pontos críticos, intervalos de crescimento e decrescimento, concavidade, pontos de inflexão e extremos locais ou absolutos.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede primeiro para esboçar o gráfico da função .
A partir disso, a questão pede várias informações sobre essa função.
Como são muitas informações, vamos devagarinho para você entender melhor, certinho? 😉
Passo 2
Bom... como se trata de uma função de grau 4, ao descobrir as raízes, encontramos o seguinte gráfico:
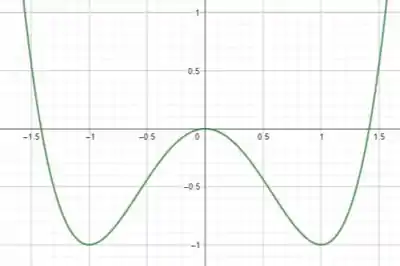
Passo 3
Bom... pelo gráfico percebemos que o domínio da função são todos os valores de em .
Passo 4
Pelo gráfico percebemos que a função é contínua para todo em .
Passo 5
Pelo gráfico percebemos que a função é derivável para todo em .
Passo 6
Temos que .
Colocando em evidência e igualando a função a zero, temos:
Portanto, temos os seguintes pontos de interseção:
Passo 7
Pelo gráfico percebemos que a função não apresenta assíntotas.
Passo 8
Pelo gráfico percebemos que:
- Pontos de crescimento: e ;
- Pontos de decrescimento: e .
Passo 9
Fazendo a derivada segunda, temos:
Em que temos como raízes.
Assim, temos os seguintes pontos de inflexão:
Passo 10
Fazendo o estudo do sinal, percebemos que:
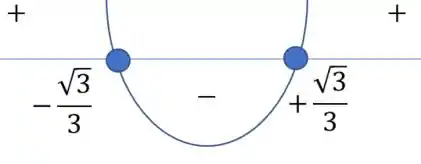
Portanto, é côncavo para cima para e é côncavo para baixo em .
Passo 11
Os extremos da função ocorrem nos pontos críticos, onde:
- Máximo:
- Mínimo: e .
Entendeu direitinho? Responde aee ;)
Resposta
No texto