UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 3
Associe as funções aos gráficos.
Passo 1
Eaí gente bonita, tudo tranquilo com vocês?
Nessa questão o enunciado nos deu funções:
E, nos pediu para associar cada uma delas ao seu respectivo gráfico.
Analisando as funções dadas vemos que elas são muito parecidas, o grande ponto é o sinal negativo, que aparece em diferentes lugares.
Assim, a nossa estratégia principal é começar determinando o gráfico da função mais simples (sem sinal negativo), , e a partir do seu gráfico vamos olhando a influência dos diferentes sinais negativos.
Beleza?! Então, vamo nessa!
Passo 2
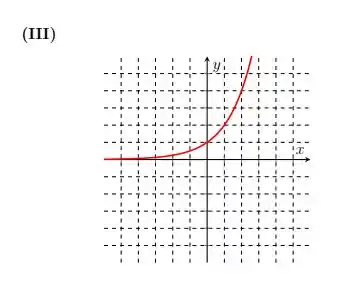
Vamos começar identificando o gráfico da função
Sabemos que trata-se de uma função exponencial. Assim, à medida que aumenta (ou seja, à direita do gráfico), a função aumenta cada vez mais. Já indo no sentido contrário, à medida que diminui, temos um valor cada vez menor de .
Além disso, essa função é sempre positiva. Assim, ela se encaixa com o gráfico:
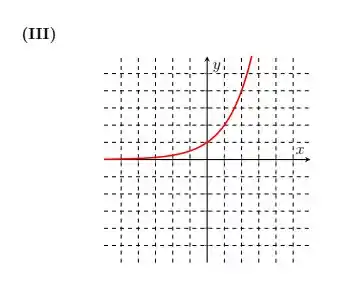
Perfeito!
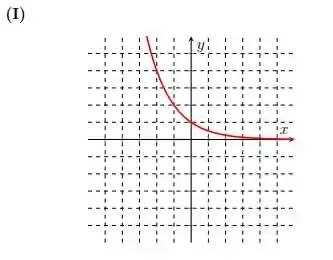
Vamos analisar agora
O que fizemos foi colocar um sinal de “menos” dentro do expoente da nossa base . Assim, invertemos o sentido de crescimento de . Antes, para os máximos valores positivos de , tínhamos os maiores valores de . Agora, em , os máximos valores de na verdade resultam nos menores valores do expoente da nossa base.
Ou seja, à medida que vamos à direita no nosso gráfico a função diminui, e à medida que vamos à esquerda ela aumenta.
É como se estivéssemos refletindo a nossa função básica com relação ao eixo . Logo, temos o gráfico:
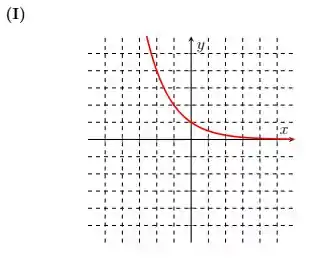
Passo 3
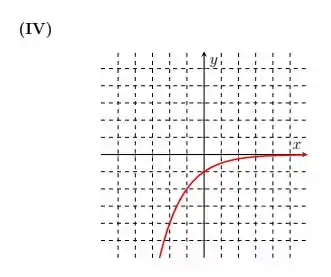
Indo pra próxima devemos analisar
Ou seja,
Já que estamos multiplicando a função por estamos apenas tornando os valores que antes eram positivos, em seus simétricos negativos. Assim, é como se estivéssemos refletindo o gráfico da função básica com relação ao eixo .
Logo, temos para o gráfico:
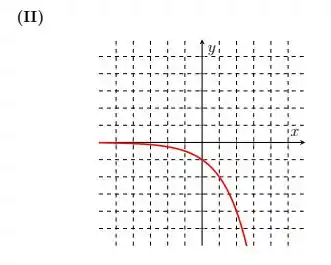
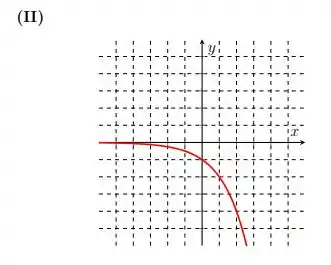
Por fim, precisamos apenas associar o último gráfico à função:
Pra fazer isso, podemos visualizar essa função como:
Ou seja, é só novamente nós refletirmos a função com relação ao eixo . Daí:
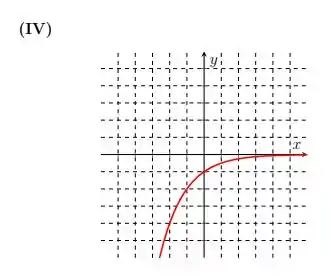
Resposta
Resposta no texto.