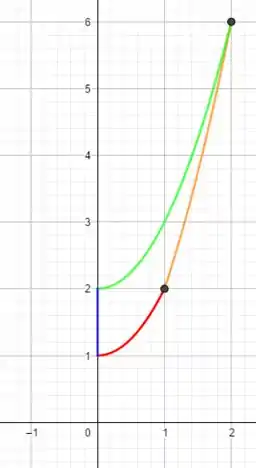
a) Esboce a região
b) Efetuando uma mudança de variáveis apropriada, calcular a integral
Dica: considerar e determinar tal que a mudança de variáveis simplifique o domínio de integração.
Passo 1
Eu prefiro desenhar cada restrição e analisar separadamente:
Essa aqui é bem de boa, teremos todo o plano onde x é positivo
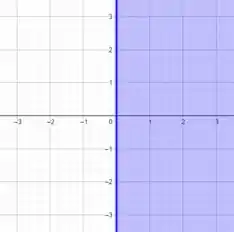
:
Para esse tipo de desigualdade é melhor você analisar como uma igualdade e depois ver a região da desigualdade.
Como essa é uma equação do segundo grau, não precisamos analisar muita coisa, apenas com alguns passos já conseguimos esboçar a nossa função. O passo a passo normalmente é o seguinte:
1)Encontrar as raizes da função que é onde a função toca nos eixos das abscissas
As raízes serão . Como temos raízes negativas, nossa função não toca no eixo
2)Econtrar onde a função toca o eixo das ordenadas :
Temos que substituir na função . Encontramos assim
3)Falta agora sabermos a concavidade:
Se o sinal do coeficiente de for positivo, a concavidade será para cima e nossa função estará feliz
Se o sinal do coeficiente de for negativo, a concavidade será para baixo e nossa função vai estar triste
Pro nosso caso ), a nossa concavidade será pra cima.
Com esse passo a passo é só marcar o ponto que encontramos: desenhar uma parábola que passe por esses pontos e com a concavidade para cima.
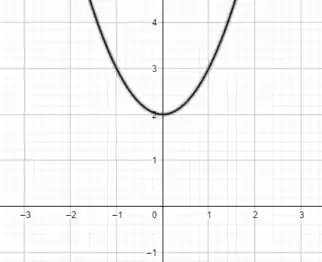
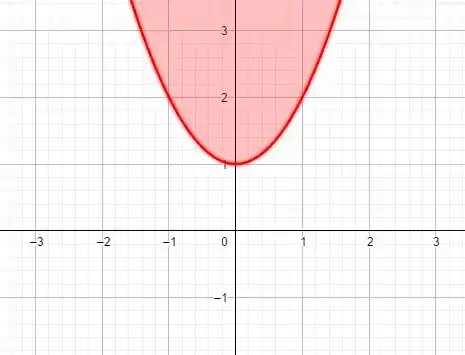
Por fim voltamos para a desigualdade. Como temos uma desigualdade de menor ou igual, a nossa região será os pontos da nossa função e todos os pontos abaixo dela. Assim:
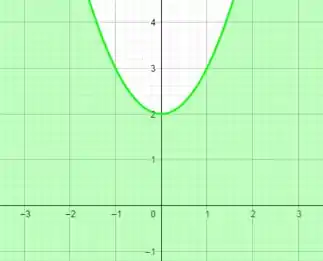
:
Similar ao que fizemos no outro só que agora ele toca o eixo em e a região vai ser acima da nossa função pois temos ali a desigualdade maior ou igual.
Vamos pro passo a passo:
1)As raízes da minha equação será: e
2)Ela encontrará o eixo no ponto
3)A concavidade será para cima
Desenhando agora a nossa região:
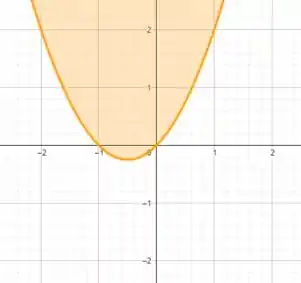
Juntando agora tudo o que a gente desenhou:
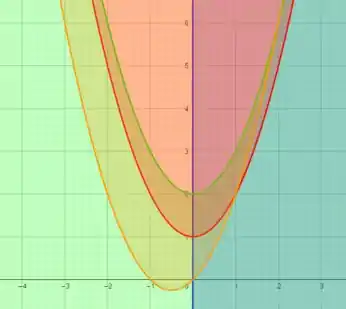
Passo 2
Para finalizar o esboço, só desenhar não é suficiente, devemos marcar os pontos onde as curvas se interceptam
Como só queremos saber onde elas se interceptam, iremos aqui considerar somente as equações:
Igualando e :
Substituindo na equação (poderíamos também substituir na ):
O ponto de interceptação será então:
Igualando agora e :
Substituindo na equação (poderíamos também substituir na ):
O ponto de interceptação será então:
Passo 3
Passo 4
Juntando tudo o que fizemos até agora nosso eboço ficará assim:
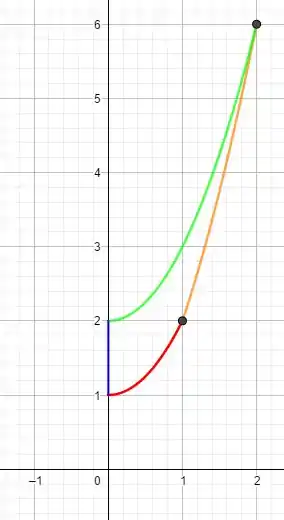
Passo 5
Resposta