UFMG, Sem Campus, Cálculo 2, Listas de Exercícios - Lista de Exercícios 5, Questão 1.6b
Esboce o desenho da curva de equação polar
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Calc 2. Nosso objetivo é esboçar a curva
Passo 2
queremos esboçar a curva polar
É o nosso famoso cardióide, mas vamos calcular alguns pontos dessa curva.
Quando
Quando
Quando
Quando
Quando
Note que existe uma simetria na curva, por conta do termo . Dessa forma, a metade da nossa curva é
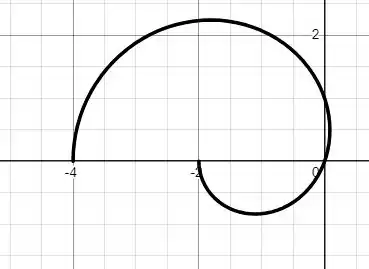
E a curva completa fica
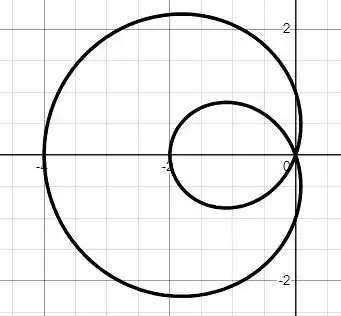
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica