UFCG, Sem Campus, Cálculo Diferencial e Integral III, Listas - Profª Pamella Queiroz - Lista 1 - 2022.1, Questão 1.2ml
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Passo 1
Oiie, tudo bem?
O enunciado nos dá duas funções, sendo elas
precisamos construir curvas de nível para cada função de forma que possamos visualizar o seu gráfico! Para isso, precisamos dar valores , em que é uma constante real! E, assim vamos montando a superfície desejada! Vamos lá!
Passo 2
Temos a seguinte função
Se igualarmos a uma constante qualquer, temos que
que é equivalente as seguintes retas
quando , e, note que devido ao módulo, quando tivermos , a relação faz com que o valor se torne novamente positivo, portanto, temos simplesmente
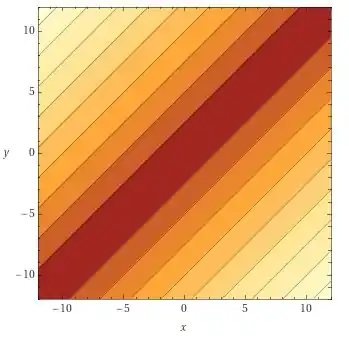
e, os gráficos são
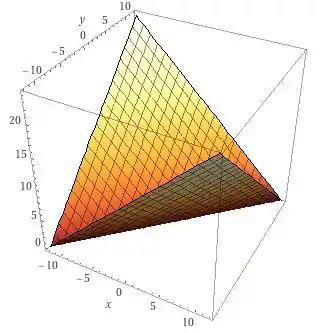
Essa foi a primeira alternativa! Vamos para a próxima agora!
Passo 3
Temos a seguinte função
igualando a uma constante qualquer, temos que
ou, simplesmente
Ou seja, temos para qualquer valor de uma reta decrescente! E, devido a estarmos analisando o módulo de , vamos ter um espelhamento quando tivermos , e portanto, , temos então
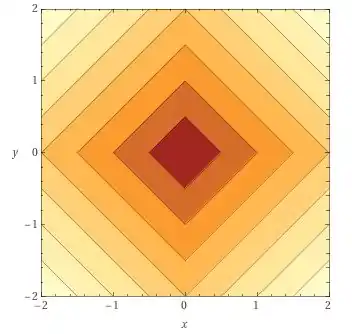
que tem o seguinte gráfico
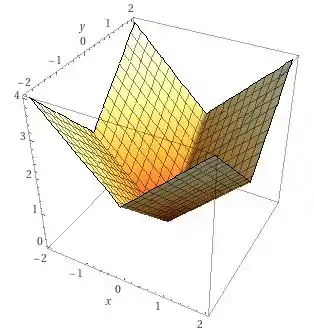
A questão foi isso! Te vejo na próxima! Tchau Tchau!